在实际问题中，我们经常会遇到多元函数的最大值、最小值问题，与一元函数类似，多元函数的最大值、最小值与极大值、极小值有密切联系.因此，先来讨论多元函数的极值问题，讨论以二元函数为主.

定义 设函数z=f(x，y)在点(x0，y0)的某个邻域内有定义，对于该邻域内异于(x0，y0)的点(x，y)都有f(x，y)＜f(x0，y0)则称 函 数f(x，y)在 点(x0，y0)有极大值f(x0，y0)，点(x0，y0)称为函数f(x，y)的极大值点.

如果对于该邻域内异于(x0，y0)的点(x，y)都有f(x，y)＞f(x0，y0)，则称函数f(x，y)在点(x0，y0)有极小值f(x0，y0)，点(x0，y0)称为函数f(x，y)的极小值点.

极大值与极小值统称为极值，极大值点与极小值点统称为极值点.例如：(1)z=x2+4y2在点(0，0)处有极小值0.

(2)z=2-在点(0，0)处有极大值2.

(3)z=xy在点(0，0)处既不取得极大值，也不取得极小值.以上关于二元函数的极值的概念很容易推广到一般的n元函数.多元函数的极值问题，一般可以利用偏导数来解决，下面两个定理就是关于这个问题的结论.

定理1 (必要条件)设函数z=f(x，y)在点(x0，y0)具有偏导数，且在点(x0，y0)处有极值，则在该点的偏导数必为零，即

(x0，y0)=0， (x0，y0)=0.

仿照一元函数，使(x，y)=0且(x，y)=0的点(x0，y0)称为z=f(x，y)的驻点.由定理1可知，具有偏导数的函数的极值点一定是驻点，但函数的驻点不一定是极值点.例如，点(0，0)是函数z=xy的驻点，但函数在该点并无极值.

怎样判断一个驻点是否为极值点呢?下面的定理回答了这个问题.

定理2 (充分条件)设函数z=f(x，y)在点(x0，y0)某个邻域内具有一阶及二阶连续偏导数，而 且(x0，y0)=0，(x0，y0)=0，令(x0，y0)=A，(x0，y0)=B.(x0，y0)=C，则f(x，y)在点(x0，y0)处是否取得极值的条件如下：

(1)B2-AC＜0时具有极值，且A＜0时有极大值，A＞0时有极小值；

(2)B2-AC＞0时没有极值；

(3)B2-AC=0时可能有极值，也可能没有极值，还需要另作讨论.

利用定理1及定理2，我们把具有二阶连续偏导数的函数z=f(x，y)的极值的求法叙述如下：

(1)解方程组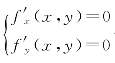，求出所有驻点(x0，y0)；

(2)对每个驻点(x0，y0)求出二阶偏导数值A，B，C；

(3)定出B2-AC的符号，由定理2判定f(x0，y0)是否为极值，是极大值还是极小值.(www.daowen.com)

例1 求出f(x，y)=x3-y3+3x2+3y2-9x的极值.

解 先解方程组

求得驻点(1，0)，(1，2)，(-3，0)，(-3，2).

再求二阶偏导数

A=(x，y)=6x+6，

B=(x，y)=0，

C=(x，y)=-6y+6.

在点(1，0)处，B2-AC=-12×6＜0且A＞0，所以函数在(1，0)处有极小值f(1，0)=-5；

在点(1，2)处，B2-AC=-12×(-6)＞0，所以函数在(1，2)处无极值；

在点(-3，0)处，B2-AC=-(-12)×6＞0，所以函数在(-3，0)处无极值；

在点(-3，2)处，B2-AC=-(-12)×(-6)＜0且A＜0，所以函数在(-3，2)处有极大值f(-3，2)=31.

与一元函数类似，可利用函数的极值来求函数的最值.

在前面我们知道，如果z=f(x，y)在有界闭区域D上连续，则f(x，y)在D上必定取得它的最大值和最小值，最值点可能在D的内部，也可能在D的边界上.我们假定，函数在D上连续、在D内可微且只有有限个驻点，这时，如果最值点在D的内部，则该点一定是极值点.因此，在上述假定下，求函数最值的一般方法是：将函数z=f(x，y)在D内的所有驻点处的函数值以及边界D上的函数值相比较，其中，最大的就是最大值，最小的就是最小值，但这种做法由于要求出z=f(x，y)在边界D上的最值，往往比较复杂，在通常遇到的实际问题中，如果根据问题的性质，知道z=f(x，y)的最大(小)值一定在区域D内部取得，且函数在D内只有一个驻点，那么，可以肯定该驻点处的函数值就是函数z=f(x，y)在D上的最大(小)值.

例2 要用铁板做一个体积为2m3的有盖长方体水箱，问当长、宽、高各取怎样的尺寸时，才能使用料最省?

解 设水箱长为x m，宽为y m，则其高为m，所用铁板面积为S，则

令

得x=为唯一驻点.根据题意可知，水箱所用材料面积的最小值一定存在，且在D：x＞0，y＞0内取得，即当长为，宽为，高为时材料最省.从这个例子可知，体积一定的长方体中，立方体的表面积为最小.