1.变力沿直线所做的功

例8 已知1N的力能使某弹簧拉长1cm，求使弹簧拉长5cm拉力所做的功.

解 取弹簧的平衡点作为原点建立坐标系，如图5-25.由胡克定律知，在弹性限度内拉长弹簧所需的力F与拉长长度x成正比，即F=kx，其中k为弹性系数.已知拉长x=1cm=0.01m，需力F=1N，于是k=100N/m.

即F=100x.

在区间[0，0.05]中任一小区间[x，x+dx]上拉力所做的功，即功的微元

dW=Fdx=100xdx，

于是拉力使弹簧拉长5cm=0.05m所做的功

例9 修建一座大桥的桥墩时先要下围囹，并且抽尽其中的水以便施工.已知围囹的直径为20m，水深27m，围囹高出水面3m，求抽尽水所做的功.

解 如图5-26，建立直角坐标系.

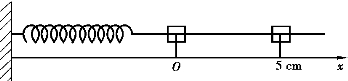
图5-25

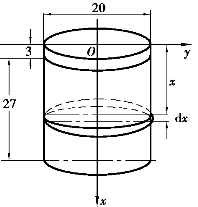
图5-26

(1)取积分变量为x，积分区间为[3，30].

(2)在区间[3，30]上任取一小区间[x，x+dx]，与它对应的一薄层(圆柱)水的质量为9.8ρ(π102dx)N.其中水的密度ρ=103kg/m3.

因这一薄层水抽出围囹所做的功近似于克服这一薄层水的重力所做的功，即功的微元为dW=9.8×105πxdx.

(3)写出定积分表达式，得所求功为

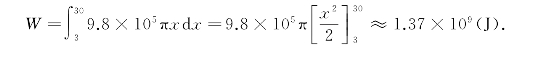
例10 设有一直径为8 m的半球形水池，盛满水，若将池中的水抽干，问至少需做多少功?

解 建立直角坐标系，如图5-27，池壁与xOy平面的交线为半圆周x2+y2=16(x≥0).

取x为积分变量，x∈[0，4].与小区间[x，x+dx]对应的是厚度为dx的一层水，这层水的体积dV≈πy2dx=π(16-x2)dx，其所受重力dG≈ρgdV=πρg(16-x2)dx，其中水的密度ρ=103kg/m3，重力加速度g=9.8m/s2，把这层水抽出，至少需提升x(单位：m)距离，故需做功至少为

ΔW≈dW=πρg(16-x2)xdx(kJ)，

因此，把水抽干需做的功至少为

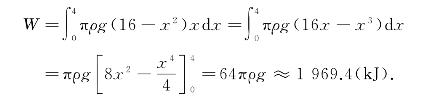
2.水压力

例11 设有一等腰三角形闸门，垂直置于水中，底边与水面相齐，已知闸门底边长为a(单位：m)，高为h(单位：m)，试求闸门的一侧所受的水压力.(水的密度ρ=1吨/m3)

解 建立坐标系(如图5-28)，则三角形的一条等腰边的方程是

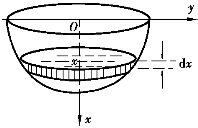
图5-27

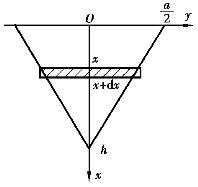
图5-28

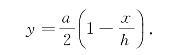
因为压强与水深成正比，同一深度的压强是相同的，于是将闸门水平分割成小横条，即取变量x为积分变量，x∈[0，h].对应小区间为[x，x+dx]，闸门上有高为dx的小条，其面积ΔA≈dA=2ydx=a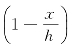dx，其上的压强近似等于gx(kN/m2)，g为重力加速度，故其上所受的水压力为

于是整个闸门所受的水压力为

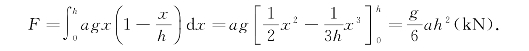
3.平均值(www.daowen.com)

我们知道：n个数y1，y2，…，yn的算术平均值为

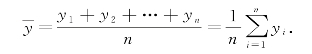
那么如何求连续函数y=f(x)在[a，b]上的平均值呢?

解决问题的思路是：将[a，b]n等分，当n很大时，每个子区间[xi，xi+Δx](i=1，2，…，n)的长度Δx=就很小，由于函数f(x)在[a，b]上连续，它在子区间[xi，xi+Δx]上的函数值差别就很小，因此可以取f(xi)作为函数在该子区间上的平均值的近似值，于是函数在[a，b]上的平均值近似为

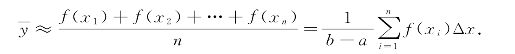
当n越大，近似值的精度越高，当n→+∞时得函数的平均值为

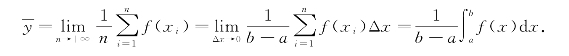
4.定积分在经济上的应用

第三章中已经介绍了经济学中常见的几种函数，如成本函数C(x)，收益函数R(x)，利润函数L(x)，需求函数Q=f(P)，又介绍了它们的导数，分别为边际成本函数C′(x)，边际收益函数R′(x)，边际利润函数L′(x)，边际需求函数Q′=f′(P).其中x表示产量、销售量、需求量，P为价格.由某一经济函数求它的边际函数是求导运算，在实际问题中也有相反的要求，即已知边际函数，需考虑对应的经济函数，这是积分运算.下面通过具体例子说明定积分在经济中的应用.

例14 每天生产某产品x单位时，固定成本为20元，边际成本函数为C′(x)=0.4x+2(元/单位).

(1)求成本函数C(x)；

(2)如果这种产品销售价为18元/单位，且产品可以全部售出，求利润函数L(x)；

(3)每天生产多少单位产品时，才能获得最大利润?

解 (1)边际成本的某个原函数C1(x)为可变成本，它满足C1(0)=0，故

习题5-5

1.求由下列各组函数所围成平面图形的面积.

(1)xy=1，y=x，x=2； (2)y=ex，y=e-x，x=1；

(3)x=y2，y=x2；　(4)y=x2，x+y=2.

2.求抛物线y=-x2+4x-3及其在点(0，-3)和(3，0)处的切线所围平面图形的面积.

3.平面图形由y=sinx(0≤x≤π)和y=0围成，试求该图形：

(1)绕x轴旋转所成旋转体的体积；

(2)绕y轴旋转所成旋转体的体积.

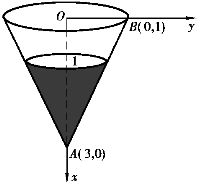
图5-29

4.平面图形由y=2x-x2和y=0围成，试求该图形分别绕x轴和y轴旋转所得旋转体的体积.

5.一物体，其底面是半径为R的圆，用垂直于底圆某一直径的平面截该物体，所得截面都是正方形，求该物体的体积.

6.一圆锥形容器放置如图5-29所示，上底半径为1m，高3m，锥中盛水深2m，如将水全部抽出，求需做功多少.

7.一块底为4m、高为3m的等腰三角形平板，铅直地置于水中，底边在上，平行于水面，位于水面下1m，求该平板的一侧受到的水的压力.

8.某下水道的横截面是直径为3m的圆，水平铺设，下水道内水深1.5m，求与下水道垂直的闸门所受的压力.

9.由胡克定律知道，弹簧的伸长与拉力成正比.已知一弹簧伸长1cm时拉力为1N，求把弹簧拉长10cm所做的功.

10.某厂每批生产某产品x单位时，边际成本为5元/单位，边际收益为10-0.02x(单位：元/单位)，当生产10单位产品时总成本为250元.问：每批生产多少单位产品时利润最大?并求出最大利润.

11.某产品的边际收益函数和边际成本函数分别为

R′(x)=18(单位：万元/t)和C′(x)=3x2-18x+33(单位：万元/t)，其中x为产量，单位为t，0≤x≤10，且固定成本为10万元，当产量x为多少t时，利润最大?并求出最大利润.

12.计算函数y=2xe-x在[0，2]上的平均值.