1.旋转体体积

一平面图形绕这平面内的一条直线旋转所成的立体称为旋转体，该直线称为旋转轴.常见的旋转体有圆柱体、圆锥体、圆台体和球体等.怎样求旋转体的体积呢?

设有一旋转体，如图5-19所示，是由连续曲线y=f(x)与直线x=a，x=b及x轴围成的曲边梯形，绕x轴旋转一周而成的旋转体，现在用微元法讨论它的体积V的计算方法.

选择x为积分变量，积分区间为[a，b].考虑小区间[x，x+dx]上小旋转体的体积ΔV，用以半径为f(x)的圆为底，高为dx的圆柱体体积π[f(x)]2dx作为近似，即得体积微元为dV=π[f(x)]2dx.

于是，旋转体的体积为V=[f(x)]2dx.

类似地，可求得由曲线x=φ(y)与直线y=c，y=d及y轴所围成的曲边梯形绕y轴旋转一周而成的旋转体的体积(如图5-20)为

图5-19

图5-20

例6 设平面图形由曲线y=2与直线x=1及y=0围成，试求：

(1)绕x轴旋转而成的旋转体体积；

(2)绕y轴旋转而成的旋转体体积.

解 (1)取x为积分变量，积分区间为[0，1]，对应于小区间[x，x+dx]的小旋转体体积为ΔV，用小矩形(如图5-21(a)中阴影部分)绕x轴旋转而成的小圆柱体(如图5-21(b))体积作为近似，即得体积微元为

于是，绕x轴旋转而成的旋转体体积为

(2)取y为积分变量，积分区间为[0，2]，对应于小区间[y，y+dy]的小旋转体体积为ΔV，用小矩形(如图5-22(a)中阴影部分)绕y轴旋转所得的空心圆柱体(如图5-22(b)所示)体积作为近似，而空心圆柱体体积等于以dy为高、半径为1的圆柱体体积减去半径为y2的圆柱体体积，即得体积微元为

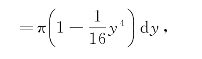(www.daowen.com)

于是，绕y轴旋转而成的旋转体体积为

图5-21

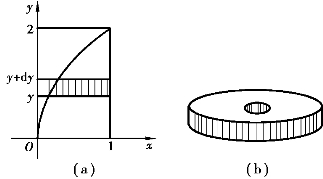
图5-22

2.平行截面面积为已知的立体体积

对于一般的空间立体，如果它与某一轴线(如x轴)相垂直的平面的截面面积A(x)(a≤x≤b)是一已知的连续函数，如图5-23所示，那么，根据微元法，可取体积微元为

dV=A(x)dx，

于是，空间立体的体积为A(x)dx.

例7 一平面过半径为R的圆柱体的底圆中心，且与底面的夹角为α，截得一楔形体(图5-24).求这楔形体的体积.

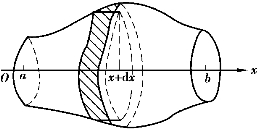
图5-23

图5-24

解 取坐标系如图5-24所示，于是底圆的方程为x2+y2=R2，任取x∈[-R，R]用过点(x，0)且垂直于x轴的平面截得的截面是一个直角三角形，它的一条直角边长度为y，另一条为ytanα，因此截面面积为

于是由上述公式，得