用定积分表示一个量，如几何量、物理量或其他的量，一般分四步来考虑，我们来回顾一下解决曲边梯形的面积的过程.

第一步分割：将区间[a，b]任意分为n个子区间[xi-1，xi](i=1，2，3，…，n)，其中x0=a，xn=b.

第二步近似代替：在任意一个子区间[xi-1，xi]上，任取一点ξi，作小曲边梯形面积ΔAi的近似值，即ΔAi≈f(ξi)Δxi.

第三步求和：得曲边梯形的面积A的近似值，A≈Δxi.

第四步取极限：n→∞，且λ=max{Δxi}→0得曲边梯形的面积

(www.daowen.com)

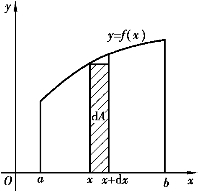
图5-10

对照上述四步，我们发现第二步近似代替时其形式f(ξi)Δxi与第四步积分(x)dx中的被积分式f(x)dx具有类似的形式，如果把第二步中的ξi用x代替，Δxi用dx替代，那么它就是第四步积分中的积分表达式，基于此，我们把上述四步简化为两步：

第一步选取积分变量，例如选为x，并确定其范围，x∈[a，b]在其上任取一个子区间记作[x，x+dx].

第二步，取曲边梯形面积A在子区间[x，x+dx]上的部分量ΔA的近似值.ΔA≈f(x)dx，如图5-10所示，f(x)dx称为面积微元，记为dA=f(x)dx.于是

上述简化了步骤的定积分方法称为定积分的微元法.