1.下列函数在区间[0，1]上是否满足拉格朗日中值定理的条件?若满足，试求出相应的ξ的值.

(1)f(x)=ex； (2)y=arcsinx.

7.欲围一个面积为150m2的矩形场地，沿矩形场地四周建筑高度相同的围墙，已知围墙正面材料价格为60元/m2，其余三面材料价格为30元/m2，问：矩形场地长x与宽y各为多少时，才能使得所用材料费T最省?

8.求下列曲线的凹凸区间与拐点.?

(1)y=(x-2)；

(2)y=ln(1+x2).

9.描绘函数y=的图形.(www.daowen.com)

10.求抛物线y=x2-4x+3在其顶点处的曲率及曲率半径.

11.曲线y=lnx上哪一点处的曲率半径最小?并求出该点处的曲率和曲率半径.

12.如图3-35，设一辆质量为m的汽车，以速度v经过抛物形拱桥.该桥跨度为l，拱高为h，试求汽车驶过拱顶O点时，汽车对桥的压力是多大?

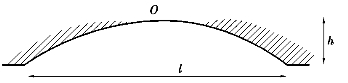
图3-35

13.某厂每年生产x台某商品的平均成本函数为(万元/台)，商品销售价格P=30万元/台，问：每年产量x为多少时，才能使得商品全部销售后获得的总利润L最大?

14.设某产品的价格与销售量的关系为P=10-，求销售量为30时的总收益、平均收益与边际收益.