在经济分析中，经常采用边际分析的方法.所谓边际分析就是利用导数来分析经济现象.

设函数y=f(x)可导，导函数f′(x)也称为边际函数.称为f(x)在(x0，x0+Δx)内的平均变化率，它表示在(x0，x0+Δx)内f(x)的平均变化速度.

f(x)在点x=x0处的导数f′(x0)称为f(x)在点x=x0处的变化率，也称为f(x)在点x=x0处的边际函数值.它表示f(x)在点x=x0处的变化速度.

在点x=x0处，x从x0改变一个单位，y相应的改变量为Δy

.但当x改变的“单位”很小时，或x的“一个单位”与x0值相对比很小时，则有Δy

=f′(x)dx

=f′(x0)(当Δx=-1时，表示x由x0减小一个单位).

边际函数值f′(x0)表示：当x=x0时，x增加一个单位，y近似改变f′(x0)个单位.在应用问题中解释边际函数值的具体意义时可略去“近似”二字.

1.边际成本

产品的成本C一般由两部分构成，一部分与产量无关，如厂房租金、设备、管理人员的工资等，称为固定成本；另一部分成本依赖于产量的大小，如生产产品所需的原材料、劳动力等等，称为可变成本.因此，总成本C是产量x的单调增加函数，称为总成本函数，记作C=C(x)(x＞0).

在生产过程中，当产品产量从x0水平增加到x0+Δx水平时，总成本函数相应的增量为ΔC=C(x0+Δx)-C(x0).

在产量区间[x0，x0+Δx]上，总成本函数对产量的平均变化率为=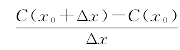.当Δx→0时，总成本函数对产量的平均变化率的极限称为总成本函数在产量x0水平上对产量的变化率，为总成本函数在点x0处对产量的导数值，即C′(x0)=.

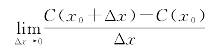一般地，考虑总成本函数在产量x水平上对产量的变化率，有下面的定义.

定义1 总成本函数C=C(x)对产量x的一阶导数C′(x)称为边际成本函数.

由定义1得，总成本函数C=C(x)在产量x0水平上对产量x的一阶导数值C′(x0)称为在产量x0水平上的边际成本值，边际成本是总成本的变化率.

在生产技术水平和生产要素的价格固定不变的条件下，产品的总成本、平均成本、边际成本都是产量x的函数.

设C为总成本，C1为固定成本，C2为可 变 成 本，为平均成本，C′为边际成本，x为产量，则有：

总成本函数　C=C(x)=C1+C2(x)；

边际成本函数　C′=C′(x).

例1 某产品的总成本函数为C=C(x)=x2+3x+6500.

求：(1)生产x0个单位产品时的总成本和平均单位成本；

(2)生产x0个到(x0+Δx)个单位产品时总成本的平均变化率；

(3)生产x0个单位产品时的边际成本，并说明其经济意义.

解 (1)生产x0个单位产品时的总成本为C(x0)=x20+3x0+6500，平均单位成本为

(2)生产x0个到(x0+Δx)个单位产品时总成本的平均变化率为

(3)生产x0个单位产品时的边际成本为

C′(x0)=(x2+3x+6500)′ x=x0=2x0+3.(www.daowen.com)

其经济意义是：当产量为x0时，再生产一个单位产品，成本将增加(2x0+3)个单位.

2.边际需求

有许多因素影响着产品的需求量，价格是影响需求量的一个基本因素，若不考虑其他因素，需求量Q是价格P的函数，则为需求函数，记为Q=f(P)，它是价格P的单调减少函数.

如果产品的需求函数为Q=f(P)，其中Q表示需求量，P表示价格，则称f′(P)为边际需求.

一般地，边际需求函数f′(P)是需求函数f(P)对销售价格P的一阶导数.

例2 已知某产品的需求函数为Q=120-，当销售价格为20元时，求产品的边际需求.

解 已知需求函数为Q=120-，边际需求函数为Q′=-，Q′(20)=-5，称为P=20时的边际需求，它表示价格P=20时，价格再上涨(下跌)一个单位，需求量将减少(增加)5个单位.

3.边际收益

设单位产品的价格为P，销售量为x，则销售总收益是销售量x的函数，称为总收益函数，记作R(x)，显然R(x)=P·x.

总收益是生产者出售一定量产品所得到的全部收入.

平均收益是生产者出售一定量产品，平均每出售单位产品所得到的收入，即单位商品的售价.

边际收益为总收益的变化率.

总收益、平均收益、边际收益均为产量x的函数.记R(x)为总收益(x)为平均收益，R′(x)为边际收益.R′(x)的经济意义是：销售量为x时，再销售一个单位产品所增加(减少)的收入.

一般地，边际收益函数R′(x)是总收益函数R(x)对销售量x的一阶导数.

4.边际利润

设销售x件产品的总收益为R(x)，这x件产品的总成本为C(x)，则R(x)-C(x)是销售量x的函数，称为总利润函数，记作L(x)，即L(x)=R(x)-C(x).

总利润函数L=L(x)，x是产量，称L′(x)为边际利润.其经济意义是：当产量为x时，再多生产一个单位产品所增加(减少)的利润.

一般地，边际利润函数L′(x)是总利润函数L(x)对产量x的一阶导数.

例3 设某厂每月生产产品的总成本C是产量x的函数：C=C(x)=0.01x2+10x+1000，如果每单位产品的售价为30元，求：

(1)总收益函数，总利润函数；

(2)边际收益，边际利润.

解 (1)总收益函数：R=R(x)=30x.总利润函数：L=L(x)=R(x)-C(x)

=30x-0.01x2-10x-1000=20x-0.01x2-1000.

(2)边际收益：R′(x)=30.

边际利润：L′(x)=20-0.02x.