我们凭直觉知道：直线是不弯曲的，半径越小的圆弯曲得越厉害，抛物线y=x2在顶点附近弯曲得比远离顶点的部分厉害些.为了定量地研究曲线的弯曲程度，先来分析曲线弯曲程度与哪些因素有关.

首先，曲线的弯曲程度与曲线的切线转角密切相关.从图3-32(a)中可以看出，曲线上动点从A沿曲线移动到B点时，其切线相应地转过了一定的角度Δα，切线转角Δα越大，则弧弯曲得越厉害.

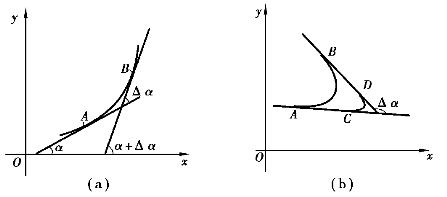
图3-32

其次，弯曲程度还与曲线的长度有关.从图3-32(b)可见，弧与弧的切线转角同为Δα，但弧长较小的比弯曲得更厉害些.

总之，曲线的弯曲程度是由切线的转角Δα和产生该转角所经过的弧长Δs两个因素所决定的，并且弯曲程度与|Δα|的大小成正比，与|Δs|的大小成反比.这里加上绝对值符号，表示只考虑曲线弯曲的程度大小，而不考虑曲线弯曲的方向.因此，我们把弧的切线转角Δα与该转角对应的弧长Δs之比的绝对值，称为该弧的平均曲率，记作，即

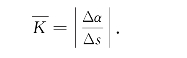
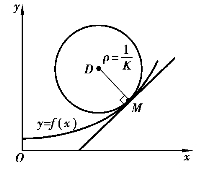
图3-33

这个结果说明：圆上任意一点处的曲率都等于常数，它正好是圆的半径R的倒数，而且半径越大，曲率越小，即圆弯曲得越不厉害；半径越小，曲率越大，即圆弯曲得越厉害.

一般地，我们把曲线y=f(x)上一点M的曲率的倒数，称为曲线在该点的曲率半径，记作ρ=(K≠0).

并且，如图3-33所示，在点M处作曲线的法线，并在曲线凹的一侧的法线上取点D，使DM=ρ，我们把以点D为圆心、ρ为半径的圆称为曲线在M点的曲率圆.

曲率圆具有如下性质：

(1)它与曲线y=f(x)在点M处相切；

(2)在M点处，曲率圆与曲线y=f(x)有相同的曲率；(www.daowen.com)

(3)在M点处，曲率圆所表示的函数与y=f(x)具有相同的一阶和二阶导数.

在实际应用中，讨论函数y=f(x)在某点x处的性质时，我们只需讨论该点处曲率圆的性质就可以了.例如，在公路工程建设中，若公路曲线为y=f(x)，车辆沿曲线弧转变时，在设计时速下的最小转弯半径为r，那么该段公路各处的曲率半径ρ必须大于r，这样才能保证车辆具有一定的速度和行车安全.

例2 计算曲线y=x3在点(0，0)与(-1，-1)处的曲率，并求在点(-1，-1)处的曲率半径.

习题3-6

图3-34

1.求曲线y=sinx的弧微分.

2.求直线y=kx+b的曲率.

3.求曲线y=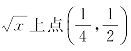处的曲率和曲率半径.

4.抛物线y=x2-2x-3上哪一点处的曲率最大?并求该点处的曲率和曲率半径.

5.如图3-34，城市轻轨列车从A处直行到O处后，须经曲线OC与曲线CB连接.试问：采用以下哪种曲线作为曲线OC更合理?请说明理由.

(1)y=ax2；

(2)x2+(y-b)2=R2；

(3)y=cx3.