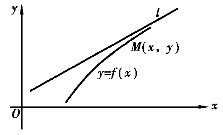
图3-24

为了完整地描绘函数的图形，除了知道其单调性、极值、凹凸性和拐点等性态外，还应当了解曲线的渐近趋向和函数的变化趋势，这个问题我们通过曲线的渐近线来讨论.

定义3 如果曲线y=f(x)上的动点M(x，y)沿着曲线无限远离坐标原点时，它与某直线l的距离趋于零，则称l为该曲线的渐近线，如图3-24所示.

如果给定曲线的方程为y=f(x)，如何确定该曲线是否有渐近线呢?如果有渐近线又怎样求出它呢?以上定义中的渐近线l可以是各种位置的直线，下面仅讨论曲线的水平渐近线和垂直渐近线.

(1)水平渐近线

如果曲线y=f(x)的定义域是无限区间，且有f(x)=b，f(x)=b或f(x)=b，则称直线y=b为曲线y=f(x)的水平渐近线，如图3-25和图3-26所示.

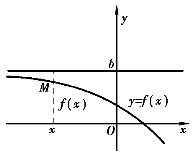
图3-25

图3-26(www.daowen.com)

(2)垂直渐近线

如果曲线y=f(x)有f(x)=∞，f(x)=∞或(x)=∞，则称直线x=a为曲线y=f(x)的垂直渐近线，如图3-27所示.

图3-27

图3-28

例6 求曲线y=的水平渐近线和垂直渐近线.

解 因为=0，所以，直线y=0是曲线y=的一条水平渐近线.

又因为=∞，所以，直线x=1是曲线y=的垂直渐近线.如图3-28所示.