如图3-21和图3-22，设函数y=f(x)是开区间(a，b)内的连续曲线，虽然它们都是上升，但图形有显著的不同.图3-21中，过上端点外的任一点作的切线，曲线弧总是位于切线上方，我们称曲线弧是(向上)凹的，或称是凹弧；图3-22中，曲线弧总是位于切线的下方，我们称曲线弧是(向上)凸的，或称为凸弧.由以上两个图形看出，两条曲线都是上升的，但凹凸性不同，下面给出曲线凹凸性的定义.

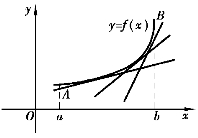
图3-21

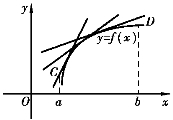
图3-22

定义1 若曲线y=f(x)在某区间内位于切线的上方，则称该曲线在此区间内是凹的，此区间称为凹区间；反之，若曲线位于其切线的下方，则称曲线在此区间内是凸的，此区间为凸区间.

如果函数f(x)在某区间(不仅闭区间，开区间也成立)内具有二阶导数，那么可以利用二阶导数的符号来判定曲线的凹凸性.

定理 设f(x)在[a，b]上连续，在(a，b)内有一阶和二阶导数，那么：

(1)若在(a，b)内f″(x)＞0，则f(x)在(a，b)的图形是凹的；

(2)若在(a，b)内f″(x)＜0，则f(x)在(a，b)的图形是凸的.

证明从略，给出如下几何说明.

当f″(x)＞0时，f′(x)随x的增大而增大，在凹弧上的各点处，切线斜率随着x的增大而增大，由图3-21可以看出，曲线是向上凹的；当f″(x)＜0时，f′(x)随x增大而减少，在凸弧上的各点处，切线斜率随着x的增大而减少，由图3-22可以看出，曲线是凸的.

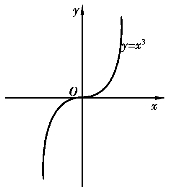
图3-23

例1 判断曲线y=x3的凹凸性.

解 因为y′=3x2，y″=6x，

当x＜0时，y″＜0，所以曲线在(-∞，0)内为凸的；

当x＞0时，y″＞0，所以曲线在(0，+∞)内为凹的.

如图3-23所示.

由例1知，点(0，0)是曲线由凸变凹的分界点.

定义2 设函数y=f(x)在某区间内连续，则曲线y=f(x)在该区间内的凹凸分界点，称为该曲线的拐点.

注意：拐点是曲线上的点，即为曲线凹凸的分界点，因此，拐点的坐标需用横坐标与纵坐标同时表示.(www.daowen.com)

如例1中，曲线y=x3的拐点为(0，0).

怎样来寻求曲线y=f(x)的拐点呢?

由f″(x)的符号可以判定曲线的凹凸性：如果f″(x0)=0，而f″(x)在x0的左、右两侧邻近异号，那么点(x0，f(x0))就是曲线的一个拐点；若f″(x)在x0的左、右两侧同号，则点(x0，f(x0))就不是曲线的拐点.因此，如果f(x)在区间(a，b)内具有二阶导数，我们就可以按下列步骤来判定曲线的凹凸性与拐点.

(1)确定函数f(x)的定义域；

(2)求f′(x)，f″(x)；

(3)令f″(x)=0，解出方程在区间(a，b)内的实根；

(4)把f″(x)=0的全部实根将定义域分成几个子区间，列表讨论在几个子区间内二阶导数f″(x)的正负号，确定函数曲线y=f(x)的凹凸区间及拐点横坐标，拐点横坐标处的函数值即为拐点纵坐标，凹用“∪”表示，凸用“∩”表示.

例2 求曲线y=6x2-x3的凹凸区间与拐点.解 函数y的定义域为(-∞，+∞)，

y′=12x-3x2，

y″=12-6x=6(2-x)，

令y″=0，得x=2，点x=2把定义域(-∞，+∞)分为两个区间：(-∞，2)，(2，+∞)，列表讨论如下：

所以曲线y=6x2-x3的凹区间为(-∞，2)，凸区间为(2，+∞)，拐点为(2，16).

例3 求曲线y=3x4-4x3+1的凹凸区间与拐点.

解 函数y的定义域为(-∞，+∞)，

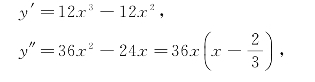
令y″=0，得x1=0，x2=.

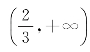x1=0及x2=把函数的定义域(-∞，+∞)分为三个区间：(-∞，0)，，列表讨论如下.