函数的极大值与极小值是局部性的概念，而最大值、最小值是全局性概念，一般来说它们是不同的.最大(小)值是函数f(x)在所考察的区间上，所有函数值中最大者(或最小者).

如果函数f(x)在闭区间[a，b]上连续，那么f(x)在[a，b]上一定有最大值和最小值.f(x)在闭区间[a，b]上的最大值(最小值)，可能在开区间(a，b)内部取得，也可能在闭区间[a，b]的端点处取得.如果f(x)的最大值(最小值)在开区间(a，b)内部取得，那么这个最大值(最小值)，也一定是一个极大值(极小值)，它们是所有极大值(极小值)中的最大(最小)者.因此，只要求出f(x)在(a，b)内的所有极值，再把它们和闭区间[a，b]端点的函数值f(a)，f(b)相比较，其中最大的就是f(x)在[a，b]上的最大值，最小的就是f(x)在[a，b]上的最小值.

由于极值点包含在驻点和导数不存在的点之中，于是，为了避免判断极值的麻烦，求函数f(x)在[a，b]上的最大、最小值可按如下步骤完成：

(1)求出f(x)在(a，b)内的所有驻点和导数不存在的点：x1，x2，…，xn；

(2)计算f(a)，f(x1)，f(x2)，…，f(xn)，f(b)的值；

(3)比较以上函数值的大小，其中最大的便是f(x)在[a，b]上的最大值，最小的便是f(x)在[a，b]上的最小值.

注意下面两种特殊情形：

(1)如果函数f(x)在[a，b]上单调增加，则f(a)是f(x)在[a，b]上的最小值，f(b)是f(x)在[a，b]上的最大值，如图3-15所示.如果f(x)在[a，b]上单调减少，则f(a)是f(x)在[a，b]上的最大值，f(b)是f(x)在[a，b]上的最小值，如图3-16所示.

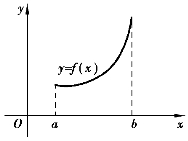
图3-15

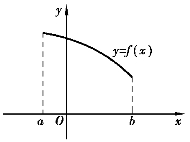
图3-16

(2)如果连续函数f(x)在区间(a，b)内有且仅有一个极大值，而没有极小值，则此极大值就是函数f(x)在区间[a，b]上的最大值，如图3-17所示.同样，如果连续函数f(x)在区间(a，b)内有且仅有一个极小值，而没有极大值，则此极小值就是函数f(x)在[a，b]上的最小值，如图3-18所示.(www.daowen.com)

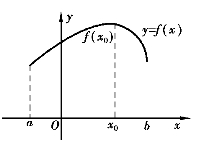
图3-17

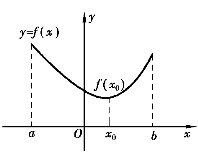
图3-18

例1 求函数y=2x3+3x2-12x+14在[-3，4]上的最大值与最小值.解 y′=6x2+6x-12=6(x+2)(x-1)，

令y′=0，得到x1=-2，x2=1.由于

f(-3)=2×(-3)3+3×(-3)3-12×(-3)+14=23，

f(-2)=2×(-2)3+3×(-2)2-12×(-2)+14=34，

f(1)=2+3-12+14=7，

f(4)=2×43+3×42-12×4+14=142，

将它们加以比较，可知在[-3，4]上的最大值为f(4)=142，最小值为f(1)=7.