由例1我们可以看到，点x1=-1及x2=1是函数y=x3-3x的单调区间的分界点.自变量x在点x1=-1的左侧邻域变到右侧邻域时，y=x3-3x的函数值由单调增加变到单调减少，在点x1=-1的左、右邻域恒有f(-1)＞f(x)，我们称f(-1)为函数f(x)的极大值.类似地，点x2=1是函数由减少变为增加的转折点，在点x2=1左右邻域恒有f(1)＜f(x)，我们称f(1)为函数f(x)的极小值.

1.极值的定义

定义 设函数y=f(x)在x0的一个邻域内有定义，如果对于该邻域内的任意一点x(x≠x0)，均有

(1)f(x0)＞f(x)，则称f(x0)为函数f(x)的极大值，x0称为f(x)的极大值点；

(2)f(x0)＜f(x)，则称f(x0)为函数f(x)的极小值，x0称为f(x)的极小值点.

函数的极大值与极小值统称为函数的极值，极大值点与极小值点统称为极值点.

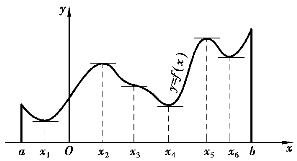
图3-8

由以上定义知，函数的极大值和极小值概念是局部性的.如果f(x0)是函数f(x)的一个极大值，那只是就x0附近的一个局部范围来说的.如果就f(x)的整个定义域来说，f(x0)不见得是最大值，关于极小值也类似.

如图3-8所示的函数f(x)，它在点x2和x5各有极大值f(x2)和f(x5)，在点x1，x4和x6各有极小值f(x1)，f(x4)和f(x6)，而极大值f(x2)小于极小值f(x6).就整个区间[a，b]来说，只有一个极小值f(x1)同时也是最小值，而没有一个极大值是最大值.

从上述图中还可以看到，在极值点处如果曲线有切线存在，并且切线有确定的斜率，那么该切线平行于x轴，即该切线的斜率等于0.但是，在某点曲线的切线平行于x轴，并不意味着这点就一定是极值点，如图3-8中的点x3不是极值点，而曲线在点x3的切线却平行于x轴.

2.极值存在的必要条件

定理2(必要条件) 设函数y=f(x)在点x0处可导，且f(x0)为极值(即x0为极值点)，则f′(x0)=0.

证明 设f(x0)为极大值，由极值定义知，必存在x0的一个邻域N(x0，δ)当x0+Δx∈N(x0，δ)时，有f(x0+Δx)-f(x0)＜0.于是

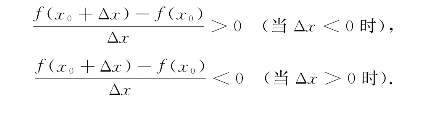
由定理条件知，f(x)在x0处可导，即f(x)在x0处的左、右导数存在且相等，f′-(x0)=f′+(x0)，所以

因此，f′(x0)=0.

同理可证极小值的情形，证明从略.

使导数为零的点(即方程f′(x)=0的实根)称为函数f(x)的驻点.

注意：(1)可导函数f(x)的极值点必定是它的驻点.但反过来，驻点可能是函数的极值点，也可能不是函数的极值点.例如，f(x)=x3的导数f′(x)=3x2，f′(0)=0，因此x=0是可导函数的驻点，但x=0却不是这个函数的极值点，如图3-9所示.

(2)定理2是对函数在点x0处可导而言的，但连续而不可导的点也可能是极值点.例如y=，显然，在x=0处连续，在该点不可导，但是x=0为该函数的极小值点，如图3-10所示.

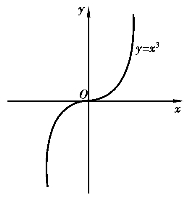
图3-9

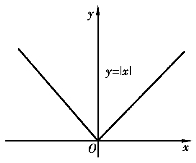
图3-10

综上所述，导数存在的极值点一定是驻点，极值点一定是驻点或不可导点，但驻点和不可导点不一定都是极值点.

3.极值存在的充分条件

定理3(极值的第一充分条件) 设函数y=f(x)在点x0的一个邻域内可导且f′(x0)=0.

(1)如果当x取x0左侧邻近的值时，f′(x)＞0，当x取x0右侧邻近的值时，f′(x)＜0，则函数f(x)在x0处取得极大值，x0为极大值点.

(2)如果当x取x0左侧邻近的值时，f′(x)＜0，当x取x0右侧邻近的值时，f′(x)＞0，则函数f(x)在x0处取得极小值，x0为极小值点.

(3)如果当x取x0左、右两侧邻近的值时，f′(x)＞0(或f′(x)＜0)，则函数f(x)在x0处没有极值.

证明 (1)根据函数单调性判别法定理1得，函数f(x)在x0的左侧邻近是单调增加的，在x0的右侧邻近是单调减少的，即有f(x0)＞f(x)，所以f(x0)是f(x)的一个极大值，如图3-11所示.

同理可证情形(2)(如图3-12所示)及情形(3)(如图3-13和图3-14所示).

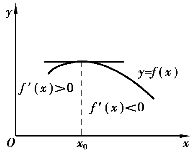
图3-11

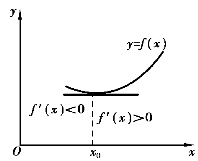
图3-12(www.daowen.com)

图3-13

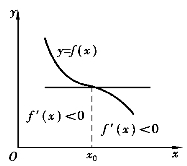
图3-14

定理3也可以这样理解：当x在x0的邻近渐增地经过x0时，如果f′(x)的符号由正变负，则f(x)在x0处取得极大值；如果f′(x)的符号由负变正，则f(x)在x0处取得极小值；如果f′(x)的符号并不改变，则f(x)在x0处没有极值.

定理4(极值的第二充分条件) 设函数y=f(x)在x0处的二阶导数存在，若f′(x0)=0，f″(x0)≠0，那么

(1)当f″(x0)＜0时，函数f(x)在x0处取得极大值，x=x0为极大值点；

(2)当f″(x0)＞0时，函数f(x)在x0处取得极小值，x=x0为极小值点；

(3)当f″(x0)=0时，不能确定f(x0)是否为极值.

证明从略.

定理4是用二阶导数的符号来判定函数f(x)在x0处的极值.由定理4知，如果函数f(x)在驻点x0处的二阶导数f″(x0)≠0，则该驻点一定是极值点，并且可以按二阶导数f″(x0)的符号来判定f(x0)是极大值还是极小值.如果f″(x0)=0，定理4就失效，这时就应运用定理3来判定.

综合以上讨论，运用定理3求函数极值的一般步骤如下：

(1)确定函数f(x)的定义域；

(2)计算一阶导数，求出驻点和导数不存在的点；

(3)函数f(x)的全部驻点和导数不存在的点(如果有的话)将定义域分成几个子区间，列表判断在这几个子区间内一阶导数f′(x)的符号，确定函数f(x)的单调性、极值点；

(4)计算极值点处的函数值，即为所求极值.

例4 求函数f(x)=x3-6x2+9x+5的极值.

解 f(x)的定义域为(-∞，+∞).

f′(x)=3x2-12x+9=3(x-1)(x-3).

令f′(x)=0，得函数f(x)的驻点x1=1，x2=3.

将x1，x2把函数的定义域分成的三个部分区间(-∞，1)，(1，3)，(3，+∞)列表讨论如下.

由上表知，函数f(x)在点x1=1处有极大值f(1)=9(极大值点为1)，在x2=3处有极小值f(3)=5(极小值点为3).

例5 求函数y=(x-3)2(x-2)的极值.

解 函数的定义域为(-∞，+∞)，

y′=2(x-3)(x-2)+(x-3)2.

令y′=0，则

2(x-3)(x-2)+(x-3)2=0，(x-3)(3x-7)=0，

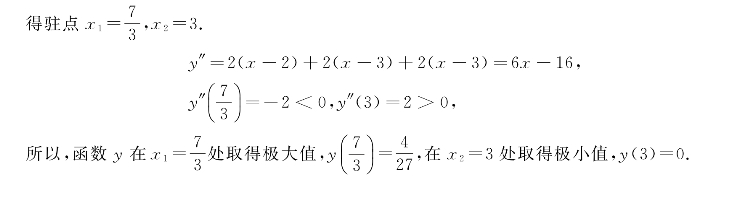
习题3-3

1.求下列函数的单调区间.

2.证明下列不等式.

3.求下列函数的极值.