如图3-5所示，如果函数y=f(x)在[a，b]上单调增加，那么它的图像是一条沿x轴正向上升的曲线.这时函数曲线y=f(x)上任意点(x，y)处切线的倾斜角α是锐角，因而切线斜率都为正值，即y′=f′(x)＞0.

如图3-6所示，如果函数y=f(x)在[a，b]上单调减少，那么它的图像是一条沿x轴正向下降的曲线.这时函数曲线y=f(x)上任意点(x，y)处切线的倾斜角β是钝角，因而切线斜率都为负值，即y′=f′(x)＜0.

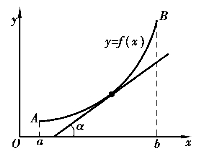
图3-5

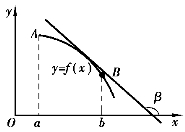
图3-6

由此可知，函数的单调性与一阶导数的符号有着密切的联系.

定理1 设函数y=f(x)在[a，b]上连续，在(a，b)内可导.

(1)如果在(a，b)内f′(x)＞0，那么函数y=f(x)在(a，b)内单调增加；

(2)如果在(a，b)内f′(x)＜0，那么函数y=f(x)在(a，b)内单调减少.

证明 在(a，b)内任取两点x1，x2，且x1＜x2，显然，函数f(x)在[x1，x2]上满足拉格朗日中值定理的条件.于是，至少存在一点ξ∈(x1，x2)，使得

f(x2)-f(x1)=f′(ξ)(x2-x1) (x1＜ξ＜x2).

(1)因为x1＜x2，所以x2-x1＞0.又因为f′(x)＞0，那么也有f′(ξ)＞0.于是f(x2)-f(x1)=f′(ξ)(x2-x1)＞0，即f(x1)＜f(x2).

这表明函数y=f(x)在(a，b)内单调增加.

(2)对于f′(x)＜0的情形，其证法与(1)的证法类似，证明从略.

注意：(1)如果将定理中的闭区间[a，b]换成其他各种区间(包括无穷区间)，定理结论仍然成立.

(2)如果将定理中的条件f′(x)＞0(或f′(x)＜0)改成f′(x)≥0(或f′(x)≤0)，但等号只在有限个点处成立，则函数f(x)在(a，b)内仍然是单调增加(或单调减少)的.

例1 求函数y=x3-3x的单调区间.解 函数的定义域为(-∞，+∞).

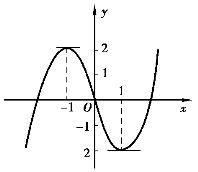
图3-7(www.daowen.com)

y′=3x2-3=3(x+1)(x-1).

令y′=0，得x1=-1，x2=1.点x1，x2把定义域分为三个部分区间：(-∞，-1)，(-1，1)，(1，+∞).

因为当x∈(-∞，-1)时，y′＞0；x∈(-1，1)时，y′＜0；x∈(1，+∞)时，y′＞0，所以在(-∞，-1)和(1，+∞)内函数y单调增加，在(-1，1)内函数y单调减少，如图3-7所示.

为了简便起见，将上述讨论归纳为如下的表格.

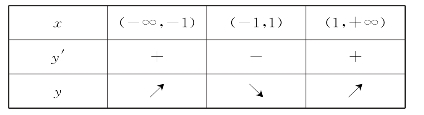
其中箭头↗，↘分别表示函数在指定区间内单调递增和单调递减.

例2 求函数y=2x3-3x2+4的单调区间.

解 函数的定义域为(-∞，+∞)，

y′=6x2-6x=6x(x-1).

令y′=0，得x1=0，x2=1.

它们将定义域分成三个部分区间：(-∞，0)，(0，1)，(1，+∞)，列表讨论如下.

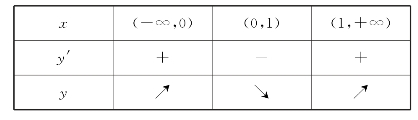
由以上表格知，函数y在(-∞，0)和(1，+∞)内单调增加，函数y在(0，1)内单调减少.

由例1、例2可得求函数的单调性的一般步骤如下：

(1)确定函数的定义域；

(2)求一阶导数，并令y′=0，求出它在定义区间内的全部实根，按从小到大的顺序排列，这些实根把定义域分为若干个子区间；

(3)判断y′在各个子区间内的符号，从而确定函数y在各个子区间内的单调性.