在罗尔定理中，第3个条件f(a)=f(b)是比较“苛刻”的，不易被一般的函数所满足，这使得罗尔定理的适用范围较窄.而事实上，若函数f(x)只满足罗尔定理的前两个条件，仍然具有与罗尔定理相类似的结论.如图3-3所示，如果连续曲线y=f(x)除端点外，处处有不垂直于x轴的切线，那么在曲线弧上至少存在一点C(ξ，f(ξ))，使曲线在该点的切线平行于过曲线两端点的弦AB.

拉格朗日中值定理 设函数f(x)满足：

(1)在闭区间[a，b]上连续，

(2)在开区间(a，b)内可导，

则在(a，b)内至少存在一点ξ，使得f′(ξ)=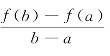(a＜ξ＜b)成立.

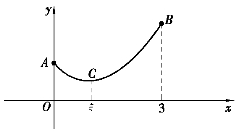
图3-2

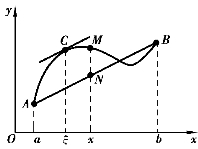
图3-3

定理的证明从略.

拉格朗日中值定理的结论往往也表示为

f(b)-f(a)=f′(ξ)(b-a)，

我们称这个式子为拉格朗日中值公式.从前面的分析中，我们不难发现：(1)拉格朗日中值定理是罗尔定理的推广，罗尔定理是拉格朗日中值定理的特殊情况.(2)在拉格朗日中值公式中，令x0=a，Δx=b-a，则公式可写成

f(x0+Δx)=f(x0)+f′(ξ)Δx (x0＜ξ＜x0+Δx)，

比较微分近似公式

f(x0+Δx)≈f(x0)+f′(x0)Δx，

可知，拉格朗日中值公式是微分近似公式的精确化表现.

作为拉格朗日中值定理的一个应用，我们可以导出在积分学中很有用的一个定理.我们知道，若函数f(x)在某区间上是一个常数时，那么f(x)在该区间上的导数恒为零，它的逆命题也是成立的，这就是：

定理 如果函数f(x)在区间I上的导数恒为零，那么f(x)在区间I上是一个常数.证明 在区间I上任取两点x1，x2(x1＜x2)，由拉格朗日中值定理有(www.daowen.com)

f(x2)-f(x1)=f′(ξ)(x2-x1) (x1＜ξ＜x2)，

由题设知f′(ξ)=0，所以f(x2)-f(x1)=0，即f(x2)=f(x1).

又因为x1，x2是I上任意两点，所以f(x)在I上的函数值总是相等的，也就是说，f(x)在区间I上是一个常数.

例1 证明：|sinb-sina|≤|b-a|.

证 设f(x)=sinx，不妨设a＜b.由于f(x)=sinx在[a，b]上满足拉格朗日中值定理的条件，所以有

sinb-sina=cosξ·(b-a) (a＜ξ＜b)，

即

|sinb-sina|=|cosξ|·|b-a|.

又因为|cosξ|≤1，所以必有|sinb-sina|≤|b-a|.

例2 证明：当x＞0时，ln(1+x)＜x.

证明 设f(x)=ln(1+x)，显然f(x)在[0，x]上满足拉格朗日中值定理的条件，根据定理应有

f(x)-f(0)=f′(ξ)(x-0) (0＜ξ＜x).

由于f(0)=0，f′(x)=，因此上式即为

又由0＜ξ＜x，有

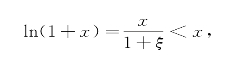
即

ln(1+x)＜x.