罗尔定理 设函数f(x)满足下列条件：

(1)在闭区间[a，b]上连续，

(2)在开区间(a，b)内可导，

(3)f(a)=f(b)，

则在(a，b)内至少存在一点ξ，使得f′(ξ)=0(a＜ξ＜b).

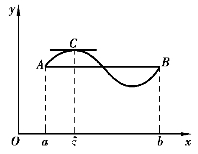
图3-1

罗尔定理的几何意义是：如图3-1所示，若连续曲线y=f(x)在端点A，B处的纵坐标相等，除端点外处处有不垂直于x轴的切线，则曲线上至少存在一点C，使得在该点处的切线平行于x轴(或弦AB).

证明 由于f(x)在[a，b]上连续，根据闭区间上连续函数的最大值和最小值定理，f(x)在[a，b]上必有最大值M和最小值m，这样只可能有两种情形：

(1)M=m，这时f(x)在[a，b]上必然取相同的数值，即f(x)=M，于是有f′(x)=0.此时，(a，b)内任意一点都可作为ξ，使f′(ξ)=0.(www.daowen.com)

(2)M＞m，因为f(a)=f(b)，所以M和m两个数中至少有一个不等于f(x)在[a，b]的端点值.为确定起见，不妨设M≠f(a)(m≠f(a)的证法完全类似)，那么必定在开区间(a，b)内有一点ξ，使f(ξ)=M.

下面证明f(x)在点ξ处的导数等于零，即证明f′(ξ)=0.

因此，必然有f′(ξ)=0.

关于罗尔定理，需要注意的是：

(1)定理中3个条件，有任何一个不满足，则定理的结论就可能不成立.

(2)定理的结论中“至少在(a，b)内存在一点ξ”，并没有指出ξ点的具体数，也没有指出ξ点在(a，b)内的位置，同时没有给出求ξ点的具体方法，只是指出了ξ点的存在性，但从后面的应用可以看出，这并不影响该定理的使用.

(3)定理的3个条件是充分非必要的，也就是说，定理的结论成立时，函数未必满足定理的3个条件，即定理的逆命题不成立.例如，函数y=(x-1)2+1在闭区间[0，3]上，如图3-2所示，f(0)≠f(3)并不满足定理中f(a)=f(b)的条件，但在(0，3)内存在一点ξ=1，使f′(1)=0.