在工程技术中，经常利用微分把一些复杂的计算公式用简单的公式来代替.

前面说过，如果当y=f(x)在x0处的导数f′(x0)≠0，且|Δx|很小时，有

Δy≈dy=f′(x0)Δx，

即

Δy=f(x0+Δx)-f(x0)≈f′(x0)Δx，

(2-11)

或

f(x0+Δx)≈f(x0)+f′(x0)Δx.

(2-12)

在式(2-12)中，令x0+Δx=x，即Δx=x-x0，那么式(2-12)又可写为

f(x)≈f(x0)+f′(x0)(x-x0).

(2-13)

如果f′(x0)及f(x0)都容易计算，那么可利用式(2-11)近似计算Δy，利用式(2-12)近似计算f(x0+Δx)，或利用式(2-13)近似计算f(x).

例7 有一批半径为1cm的球，为了提高球面的光洁度，要镀上一层厚度为0.01cm的铜，估计每只球需用铜多少克?(铜的密度是8.9g/cm3)

解 先求出镀层的体积，再乘以密度就得到每只球需用铜的质量.

镀层的体积等于两个球体体积之差，即球的体积V当半径R由R0增加到R0+ΔR时，体积的增量为ΔV.

由于

所以

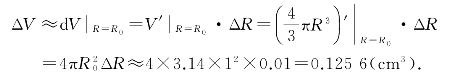
于是每只球需用铜的质量约为

0.1256×8.9≈1.118(g).(www.daowen.com)

例8 利用微分计算sin30°30′的近似值.

解 把30°30′化为弧度，得

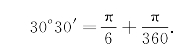
由于所求的是正弦函数的值，故设f(x)=sinx，从而f′(x)=cosx.

习题2-5

1.单项选择题.

2.求下列函数的微分.

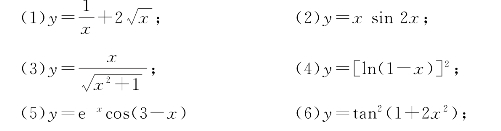
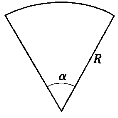
图2-7

3.在下列括号内填入适当的函数，使等式成立.

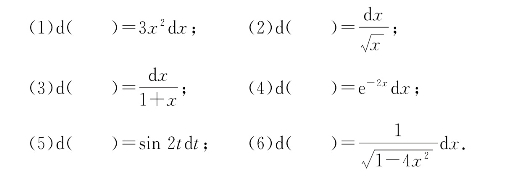
4.利用微分求下列函数的近似值.

5.已知单摆的振动周期T=2π，其中g=980cm/s，l为摆长(单位为cm).设摆长为20cm，为使周期T增大0.05s，摆长约需加长多少?

6.设扇形的圆心角α=60°，半径R=100cm(图2-7).如果R不变，α减少30′.问：扇形的面积大约改变了多少?又如果α不变，R增加1cm，问：扇形的面积大约改变了多少?