图2-5

先考察一个具体问题：设一边长为x的正方形的面积A=x2是x的函数.若边长由x0增加Δx，相应地，正方形的面积的增量ΔA=(x0+Δx)2-x20=2x0·Δx+(Δx)2.它由两部分组成，第一部分2x0Δx是Δx的线性函数(即图2-5的单斜线部分的面积)，第二部分(Δx)2，当Δx→0时是比Δx的高阶无穷小，即(Δx)2=o(Δx)，即图2-5的双斜线部分的面积.由此可见，如果正方形的边长改变很微小，即很小时，面积的改变量ΔA可近似地用第一部分来代替.

一般地，函数y=f(x)当自变量在x0处有增量Δx时，则相应地函数的增量为

Δy=f(x0+Δx)-f(x0).

定义 设y=f(x)是定义在某区间上的函数，x0及x0+Δx在该区间内，如果函数的增量可表示为

Δy=AΔx+o(Δx)

(2-7)

其中A是不依赖于Δx的常数，o(Δx)是当Δx→0时较Δx的高阶无穷小，那么称函数y=f(x)在点x0处是可微的，式(2-7)中的AΔx称为函数y=f(x)在点x0处的微分，记作dy ，即

由定义可见，函数的微分与增量仅相差一个较Δx的高阶无穷小.因为dy是Δx的线性函数，所以当Δx≠0时，称dy是Δy的线性主部 .

函数y=f(x)在x0处的可导与可微有如下关系：

定理 函数f(x)在x0处可微的充分必要条件是函数f(x)在x0处可导.

证明 必要性：因为f(x)在x0处可微，由式(2-7)有

Δy=AΔx+o(Δx)，

等式两边同除以Δx后取极限得

所以f(x)在x0处可导.

充分性：因为函数y=f(x)在x0处可导，即

由极限与无穷小的关系，得

其中，α是当Δx→0时的无穷小，于是

Δy=f′(x0)Δx+α(Δx).

因αΔx=o(Δx)，且f′(x0)不依赖于Δx，故上式相当于(2-7)式.

所以f(x)在x0处可微，且有

(www.daowen.com)

由上可知，一元函数的可导与可微是等价的.

所以，当|Δx|很小，f′(x0)≠0时，有

Δy≈dy.

例1 求函数y=x2在x=1和x=3处的微分.

解 dy =2Δx；

dy=6Δx.

图2-6

微分的几何解释如图2-6所示，当自变量由x0增加到x0+Δx时，函数的增量为

而曲线y=f(x)在点x0处的切线的增量是

即函数y=f(x)在x0处的微分是曲线y=f(x)在x0处的切线的纵坐标的增量.

若函数y=f(x)在区间I上每点可微，则称f(x)为I上的可微函数.函数y=f(x)在I上的微分记作

dy=f′(x)Δx，

(2-9)

它不仅依赖于Δx，还依赖于x.

例2 设y=x，则

dy=dx=(x)′Δx=Δx.

由此可得，自变量的微分dx等于自变量的增量Δx，所以(2-9)式可写为

dy=f′(x)dx，

(2-10)

即函数的微分等于函数的导数与自变量的微分的乘积.

如果将式(2-10)写成

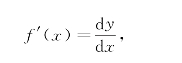
那么，函数的导数就等于函数的微分与自变量的微分的商，即导数等于微商.