1.导数的几何意义

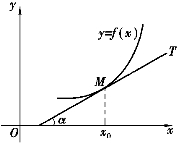
图2-2

从曲线的切线斜率的讨论及导数的定义可以知道，曲线y=f(x)在点M(x0，y0)处的切线斜率是函数y=f(x)在x0处的导数，这就是导数的几何意义，即

其中，α是切线MT的倾斜角(如图2-2).如果y=f(x)在点x0

处的导数为无穷，这时曲线y=f(x)的割线以垂直x轴的直线x=x0为极限，即曲线y=f(x)在点M(x0，y0)处有垂直于x轴的切线x=x0(可参考例5).

根据导数的几何意义并应用直线的点斜式可知，曲线y=f(x)在点M(x0，y0)处的切线方程为

y-y0=f′(x0)(x-x0)，

法线方程为

例4 求曲线y=sinx在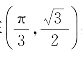处的切线与法线方程.

解 根据导数的几何意义，所求切线的斜率为

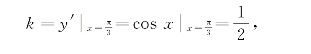(www.daowen.com)

故所求切线方程为

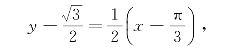
即

法线方程为

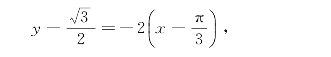
即

2.导数的物理意义

对于不同的物理量，导数的物理意义不同.如：

(1)变速直线运动路程函数s=s(t)的导数就是速度，即s′(t)=v(t).

(2)Q=Q(t)是通过导体某截面的电量，它是时间t的函数，Q(t)对时间的导数就是电流，即Q′(t)=I(t).

(3)M=M(x)是质量分布函数，它是长度x的函数，M(x)对长度x的导数就是质量非均匀分布的细杆在x处的线密度，即M′(x)=ρ(x).