上述两个例子，一个是几何问题，一个是物理问题，它们的实际意义不同，但从数量关系来分析，却是相同的，都是研究函数的增量与自变量增量比的极限问题.这类问题在科学技术中经常遇到，也正是这类问题的研究促进了导数概念的诞生.

定义2 设函数y=f(x)在x0的一个邻域内有定义，当自变量x在x0处有增量Δx(x0+Δx仍在该邻域内)时，相应的函数的增量Δy=f(x0+Δx)-f(x0).若y=f(x)当Δx→0时，的极限存在，则称函数y=f(x)在点x0处可导，并称这个极限值为函数y=f(x)在x0处的导数，记为，即

或记为f′(x0).

函数y=f(x)在点x0处可导有时也说成函数y=f(x)在点x0处具有导数或导数存在.如果式(2-1)的极限不存在，则函数y=f(x)在点x0处不可导或不具有导数或导数不存在.如果不可导的原因是由于Δx→0时，→∞，这时，为了方便起见，称y=f(x)在点x0处的导数为无穷.

导数的定义式也可以是以下形式，常见的有

和

式(2-3)中的h是自变量的增量.

由导数的定义，上述两个例子可以叙述为：

曲线y=f(x)在x0处的切线的斜率就是函数y=f(x)在x0处的导数，即k=f′(x0).(www.daowen.com)

变速直线运动s=s(t)在t0时刻的瞬时速度就是s=s(t)在t0处的导数，即v=s′(t0).

定义3 如果存在，则称这个极限值为函数y=f(x)在x0处的左导数，记为f′-(x0).同样，如果存在，则称这个极限值为函数y=f(x)在x0处的右导数，记为f′+(x0).定理1函数y=f(x)在点x0处可导的充分必要条件是函数y=f(x)在点x0处的左、右导数都存在且相等.上面所述的是函数在某一点处的导数.如果函数y=f(x)在开区间I内的每一点处都可导，就称函数f(x)在区间I内可导 .这时，对于区间I内的每一个确定的点x，都对应着f(x)的一个确定的导数值，这样就构成了一个新的函数，这个函数称为原来函数y=f(x)的导函数，也简称为导数 ，记为y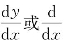′，f′(x)，f(x).

在式(2-1)和式(2-3)中，把x0换成x，即得导函数的定义式

或

注意：在以上两式中，x虽然可以取区间I内的任何数值，但在求极限过程中，x是常数，Δx或h是变量.

函数y=f(x)的导函数f′(x)与函数y=f(x)在x0处的导数f′(x0)既有区别又有联系.它们的区别在于：前者是一个函数，后者是一个数值.它们的联系在于：在x=x0处的导数值f′(x0)就是导函数f′(x)在x=x0处的函数值，即f′(x0)=f′(x)|x=x0.

定义4 如果函数既在(a，b)内可导，又f′+(a)，f′-(b)存在，则称函数f(x)在闭区间[a，b]内可导.