如果函数f(x)在点x0处不满足连续的条件，则称函数f(x)在点x0处不连续或间断.点x0称为函数f(x)的不连续点或间断点.

显然，如果函数f(x)在点x0处有以下3种情形之一，则点x0为f(x)的间断点：

(1)f(x)在点x0处没有定义；

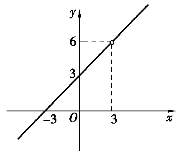
图1-10

对于这个函数我们注意到，当x→3时极限是存在的.

例6 讨论函数f(x)=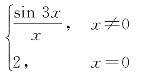

在x=0处的连续性.

解 因为函数f(x)在x=0处有定义，且f(0)=23.

由于f(x)=3≠f(0)=2，所以点x=0为该函数的间断点.

在点x0处极限存在，这样的间断点x0称为可去间断点.

如例5中的点x=3及例6中的点x=0都是可去间断点.

例7 讨论函数f(x)=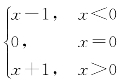

在点x=0处的连续性.

解 函数f(x)虽在点x=0处有定义，但

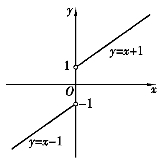
图1-11

即在点x=0处左右极限不等，所以limx→0f(x)不存在，因此，点x=0是该函数的间断点(如图1-11).

在点x0处函数左、右极限存在但不相等的间断点，称为跳跃间断点.

可去间断点与跳跃间断点统称为第一类间断点，其余间断点都称为第二类间断点.

例8 讨论函数f(x)=在点x=0处的连续性.

解 因为函数f(x)=在点x=0处没有定义，所以点x=0是该函数的间断点.

对于这个函数我们注意到，=∞，即当x→0时，函数f(x)=是无穷大.

这样的间断点属于第二类间断点，也称无穷间断点.

三、闭区间上连续函数的性质

定理1(最大值和最小值定理) 如果函数f(x)在闭区间[a，b]上连续，则函数f(x)在(www.daowen.com)

图1-12[a，b]上必有最大值和最小值.

这就是说，在[a，b]上至少有一点ξ1和一点ξ2，使得对于[a，b]上的一切x值，有

f(ξ2)≤f(x)≤f(ξ1).

这里f(ξ1)，f(ξ2)分别称为函数f(x)在闭区间[a，b]的最大值和最小值(如图1-12).

开区间内的连续函数不一定有此性质.

例如，y=x在开区间(1，2)内连续，但它在(1，2)内既无最大值又无最小值.

若函数在闭区间上有间断点，也不一定有此性质.

例如，函数f(x)=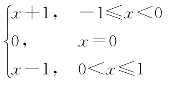在闭区间[-1，1]上有间断点x=0，而它在闭区间[-1，1]上无最大值和最小值(如图1-13).

定理2(介值定理) 如果函数f(x)在闭区间[a，b]上连续，m，M分别为f(x)在[a，b]上的最小值和最大值，则对于满足m≤μ≤M的任何实数μ，至少存在一点ξ∈[a，b]，使得f(ξ)=μ.

定理的几何意义可以由图1-14中看出，水平直线y=μ(m≤μ≤M)与[a，b]上的连续曲线y=f(x)至少相交一次.如果交点的横坐标x=ξ(图中ξ1，ξ2都可取作ξ)，则有f(ξ)=μ.

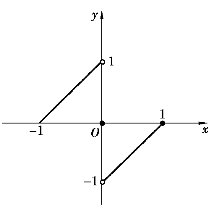
图1-13

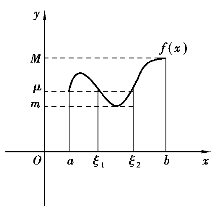
图1-14

推论(零点定理) 如果函数f(x)在闭区间[a，b]上连续，且f(a)与f(b)异号，则至少存在一点ξ∈(a，b)，使得f(ξ)=0.

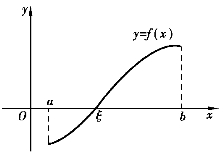
图1-15

这里因为f(a)与f(b)异号，μ=0就是在f(a)与f(b)之间的一个值，根据介值定理就可得到这一结论.

其几何意义为：连续曲线y=f(x)的端点在x轴的两侧时，曲线与x轴至少相交一次(如图1-15).

例9 证明：三次代数方程x3-4x+1=0在区间(0，1)内至少有一个实根.

证明 设f(x)=x3-4x+1，因为函数f(x)是初等函数，定义域是(-∞，+∞)，因此它在闭区间[0，1]上连续.

又因为函数在区间[0，1]的端点处的函数值分别为f(0)=1＞0，f(1)=-2＜0，根据介值定理的推论，至少存在一点ξ∈(0，1)，使f(ξ)=0.

此即说明方程x3-4x+1=0在(0，1)内至少有一个实根ξ.

习题1-8