先引入函数改变量的概念.

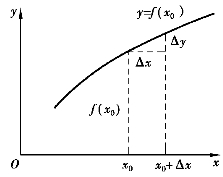
图1-9

设函数y=f(x)(如图1-9)在x0的邻域内有定义，当自变量x在该区间内由x0变到x1时，差x1-x0称为自变量x在点x0处的改变量(或增量)，记作Δx(它可正可负)，于是Δx=x1-x0，x1=x0+Δx，差f(x1)-f(x0)称为函数f(x)对应的改变量，记作Δy，即

Δy=f(x1)-f(x0)=f(x0+Δx)-f(x0).

下面考察函数f(x)在某点x0处连续的特征.

从直观上看，连续函数的图像是一条没有间断的曲线(如图1-9)，设函数f(x)的图像在点x0及其附近有定义且不发生间断，由图1-9不难看出，当自变量x在点x0处取得极其微小的改变量Δx时，函数的改变量Δy=f(x0+Δx)-f(x0)也极其微小，即当Δx→0时，Δy→0.

定义1 设函数y=f(x)在点x0及其附近有定义，且有

则称函数y=f(x)在点x0处连续，点x0称为函数f(x)的连续点.

令x0+Δx=x，则当Δx→0时，x→x0，因此上述定义中的第二式可改写成

所以，函数y=f(x)在点x0处连续的定义还可叙述如下.

定义2 设函数y=f(x)在点x0及其附近有定义，且有

则称函数y=f(x)在点x0处连续.

例1 证明函数f(x)=x3在点x=2处连续.

证明 因为f(x)=x3在点x=2及其附近有定义，且limx→2x3=8=f(2)，所以f(x)=x3在点x=2处连续.

由定义可知，f(x)在点x0连续必须同时满足以下3个条件：

(1)函数f(x)在点x0处有定义；

(2)函数f(x)的极限 f(x)存在；

(3)这个极限值等于函数值f(x0).(www.daowen.com)

如果函数f(x)在开区间(a，b)内的每一点连续，则称f(x)在开区间(a，b)内连续.如果函数f(x)在开区间(a，b)内连续，且在端点a处右连续，b处左连续，即

则称f(x)在闭区间[a，b]上连续，f(x)称为[a，b]上的连续函数.函数f(x)的连续点全体构成的区间称为该函数的连续区间.在连续区间上，连续函数的图像是一条连续不断的曲线.

例2 证明y=sinx在区间(-∞，+∞)内是连续函数.

证明 对于任意x∈(-∞，+∞)，

因为

所以

又因为x∈(-∞，+∞)内的任意点，所以y=sinx在(-∞，+∞)内连续.

连续函数具有下面的运算法则：

法则1 如果f(x)，g(x)都在点x0处连续，则f(x)±g(x)，f(x)·g(x)，(g(x)≠0)都在点x0处连续.

法则2 设函数y=f(u)在u0处连续，又函数u=φ(x)在点x0处连续，且u0=φ(x0)，则复合函数y=f[φ(x)]在点x0处连续.

这个法则说明了连续函数的复合函数仍为连续函数，并可得到如下结论：

这表示，连续函数的极限符号与函数符号可以交换次序.

法则3 单调连续函数的反函数在其对应区间上也是单调连续的.

根据上述法则可以证明：初等函数在其定义区间内是连续的.

因此，在求初等函数在其定义域内某点处的极限时，只需求在该点的函数值即可.