无穷小虽然都是以零为极限的函数，但不同的无穷小趋向于零的“速度”却不一定相同，有时可能差别很大.

例如，当x→0时，x，2x，x2都是无穷小，但它们趋向于零的速度却不一样，见表1-3.

表1-3

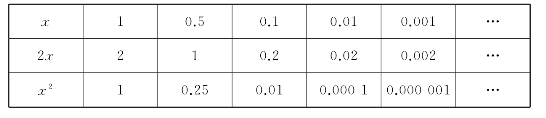
显然，x2比x与2x趋向于零的速度快得多.然而，快慢是相对的，是相互比较而言的.下面考察两个无穷小之比的极限的各种不同情况，以此作为判断的依据，特引进如下定义.

定理1表明，当α(x)～β(x)时，由β(x)代替α(x)引起的误差相比α(x)要小得多.因此，当|x|很小时(记为|x|＜＜1)，下列近似公式的误差很小：

定理2 设当x→x0时，α～α′，β～β′，且.

定理2表明，求两个无穷小之比的极限时，分子及分母都可用等价无穷小来代替.因此，如果用来代替的无穷小选得适当的话，可以使计算简化.(www.daowen.com)

当x以其他方式变化时，如x→∞，x→等，定理中的结论仍成立.

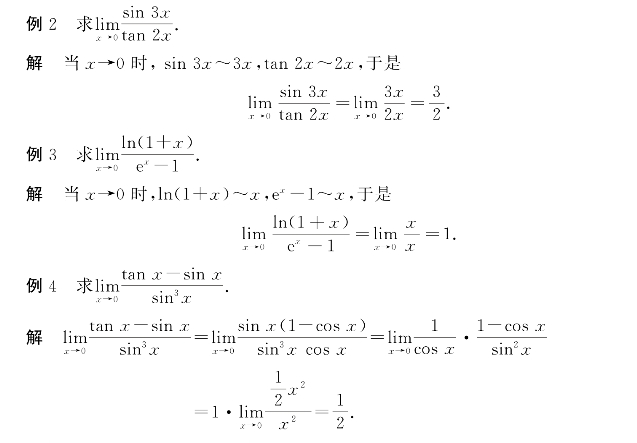
在例3中，我们是对分子和分母采用整体的无穷小替换.对于例4，若一开始就由sinx～x，tanx～x对原式作无穷小替换，则将导致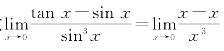=0的错误结果，读者应十分留意.

习题1-7

1.试比较下列各对无穷小的阶.

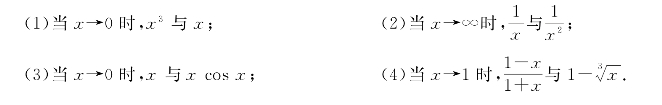
2.利用等价无穷小求下列极限.