有一类函数，从变化的规律来看，也有一定的趋势，但不是趋向于某一常数，而是在变化过程中其绝对值无限变大，如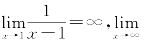x3=∞.

对于这一性态，我们给出如下定义.

定义2 若当x→x0(或x→∞)时，|f(x)|无限增大，则称函数f(x)为当x→x0(或x→∞)时的无穷大量，简称为无穷大，记作

如果当x→x0(或x→∞)时，f(x)保持正值且无限增大，则称f(x)为正无穷大，记作

同样，如果f(x)保持负值，但绝对值无限增大，则称f(x)为负无穷大，记作

例如：

注意：切不可把无穷大理解为“很大的一个数”.

无穷大与无穷小之间有一种简单的关系如下.(www.daowen.com)

定理2 在自变量的同一变化过程中，如果f(x)为无穷大，则为无穷小；反之，如果f(x)为无穷小且f(x)≠0，则为无穷大.

关于无穷小和无穷大，还应注意：

说一个函数是无穷小或无穷大时，必须指明自变量的变化趋向.例如，同一函数，当x→1时，它是无穷大；当x→∞时，它是无穷小；当x→0时，它的极限是-1，既不是无穷小，也不是无穷大.

习题1-4

1.观察下列函数，哪些是无穷小?哪些是无穷大?

2.函数f(x)=在什么条件下是无穷大?在什么条件下是无穷小?

3.函数y=xsinx当x→∞时是无穷大吗?