现在讨论x无限接近于某一个确定的数x0，且x≠x0时，函数f(x)的变化趋势.

定义2 设函数在点x0的附近有定义(点x0可除外)，若对于预先给定的任意小正数ε，总存在一个正数δ，使得当0＜|x-x0|＜δ时，不等式

|f(x)-A|＜ε (A是确定的常数)

恒成立，则称A是函数y=f(x)当x→x0时的极限，记作

定义2告诉我们，一个在x0附近有定义的函数f(x)，如x无限接近x0时，函数f(x)无限地接近一个常数A，则常数A就是x趋向x0时函数f(x)的极限.

例4 考虑当x→2时，函数f(x)=3x-1的极限.

解 由图1-6看到，当x无限接近于2时，f(x)无限接近于5，因此limx→2(3x-1)=5.

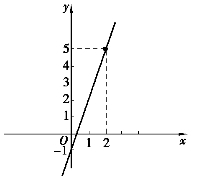
图1-6

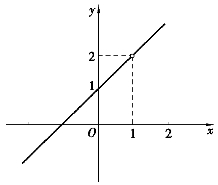
图1-7

例5 考虑x→1时，函数f(x)=的极限.

解 函数在x=1处没有定义，但是它的极限存在.

事实上，当x≠1时，f(x)=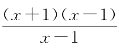=x+1，从图1-7可看到，当x→1时，f(x)→2，故

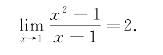
例6 试求函数

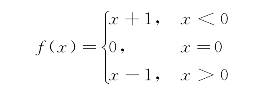
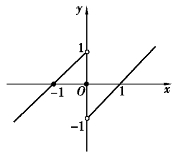
图1-8

当x→0时的极限.

解 从图1-8看到，x从0的左边趋向于0时，f(x)趋向于1；x从0的右边趋向于0时，f(x)趋向于-1，因此，当x趋向于0时，函数值没有确定的变化趋势.(www.daowen.com)

故在x→0时，函数f(x)的极限不存在.

从这个例子可以看到，虽然函数f(x)在x=0处没有极限，但当x从点x=0的某一侧趋近于0时，函数y还是分别趋近于确定的常数，由此引出单侧极限的定义.

定义3 如果当x从x=x0的左侧(即x＜x0)无限趋于x0时，函数f(x)无限趋近于常数A，则称A是函数f(x)在点x0处的左极限，记作

类似地，定义右极限

根据极限、左极限和右极限的定义，可以得出下面的定理.

定理1 函数f(x)在点x0处极限存在的充分必要条件是在该点的左、右极限都存在并且相等，即

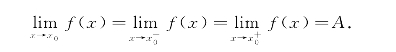
这个定理可以用来判别函数的极限是否存在.

例7 判断函数f(x)=在x→0时的极限.

解 因为

左、右极限虽然都存在，但不相等，所以f(x)=在x→0时的极限不存在.

习题1-3

1.求下列函数极限.

2.求当x→∞时，y=的极限.

3.证明：函数f(x)=|x|当x→0时极限为零.

4.求f(x)=，φ(x)=当x→0时的左、右极限，并说明它们在x→0时的极限是否存在.