1.函数概念

定义1 设D是非空实数集，如果对于D中的每一个x，按照某个对应法则f，都有确定的y与之对应，则称y是定义在D上的x的函数，记作y=f(x).D称为函数的定义域，x称为自变量，y称为因变量.

如果x0是函数y=f(x)的定义域中的一个值，则称函数y=f(x)在点x0有定义.函数在点x0的对应值称为函数在该点的函数值，记作f(x0)或.当自变量x在定义域内取每一个数值时，对应的函数值的全体称为函数的值域，记作W.

例1 函数y=的定义域为D=(-∞，0)∪(0，+∞)，值域为W=(-∞，0)∪(0，+∞)，其图形为等轴双曲线，如图1-1所示.

例2 函数y=x3的定义域D=(-∞，+∞)，值域W=(-∞，+∞)，其图形为立方抛物线，如图1-2所示.

通过对函数的定义和以上各例题的分析讨论不难发现，确定一个函数，起决定作用的因素是：

(1)对应法则f(即因变量y对于自变量x的依存关系)；

(2)定义域D(即自变量x的变化范围).

如果两个函数“对应法则f”和“定义域D”都相同，那么这两个函数就是相同的(或称相等的)；否则就是不相同的.

图1-1

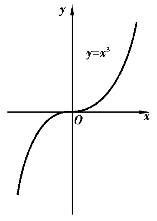
图1-2

例3 下列各对函数是否相同?为什么?

(1)f(x)=lgx2，g(x)=2lgx；

(2)f(x)=x，g(x)=；

(3)f(x)=，g(x)=x；

(4)f(x)=1-cos2x，g(x)=sinx.

解 (1)不相同.Df=(-∞，0)∪(0，+∞)，Dg=(0，+∞)，两个函数的定义域不同，因此f(x)与g(x)不相同.(www.daowen.com)

(2)不相同.f(-1)=-1，g(-1)=1，两个函数的对应法则不同，因此f(x)与g(x)不相同.

(3)相同.其定义域均为(-∞，+∞)，对应法则也相同，因此f(x)与g(x)相同.

(4)不相同.虽然两个函数的定义域都是(-∞，+∞)，但其对应法则不同，f(x)的值域是Wf=[0，1]，g(x)的值域是Wg=[-1，1]，因此f(x)与g(x)不相同.

2.函数的表示方法

函数有3种表示方法：解析法、列表法和图像法.

在实际问题中，上述3种方法常结合应用.

3.分段函数

有时一个函数要用几个式子表示，这种在自变量的不同变化范围中，对应法则用不同的式子来表示的函数，称为分段函数.

例4 函数

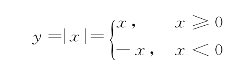
的定义域D=(-∞，+∞)，值域W=[0，+∞)，它的图形如图1-3所示，该函数称为绝对值函数.

例5 函数

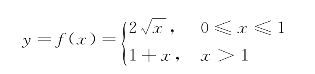
是一个分段函数，它的定义域D=[0，+∞).当x∈[0，1]时，对应的函数值f(x)=2 x；当x∈(1，+∞)时，对应的函数值f(x)=1+x.例如，∈[0，1]，所以f=2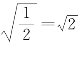；1∈[0，1]，所以f(1)=2=2；3∈(1，+∞)，所以f(3)=1+3=4.该函数的图形如图1-4所示.

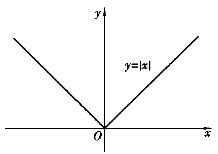
图1-3

图1-4