1.十进制

十进制在我们日常生活非常的常见，在生活中应用最多的也是十进制，十进制数中，十进制数的每一位的取值范围只能是0～9，所以计数的基数就是10，如果某一位超过9，则必须用多位数进行表示，其中低位和相邻高位之间的运算关系遵守“逢十进一”，故称为十进制。例如：

147.75=1 x 102+4x 101+7x 100+7x 10−1+5x 10−2

从上表达式可以看出：任何一个十进制数D 均可以展开为：

D=Σnix 10i

表达式中的ni是第i 为的系数，它可以使0～9 这10 个数中的任何一个。如果整数部分的位数是k，小数部分的位数是m，那么表达式中从k-1 到0 的所有正整数和从-1 到-m所有的负整数。

如果上面表达式中用N 来表示10 的话，那么任意十进制数的展开公式为：

D=ΣkiNi

其中i 的取值和上面的取值是一样的，都是从0～9 取任何一个数值，N 称为计数的基数，ki为第i 位的系数，Ni称为第i 位的权。

判断一个数是不是十进制，主要判断其每一位是不是都在0～9 范围内，比如：18、20、995、8854 等这些都是十进制数。

2.二进制

二进制目前是在各个应用领域非常广的一种数制，在二进制数中，每一位只能从0 和1取值，所以二进制数的基数是2，其中低位和相邻高位之间的运算关系遵守“逢二进一”，故称为二进制。例如：

(101.1)2=1 x 22+0x 21+1 x 20+1 x 2−1= (5.5)10

从上面的表达式可以得出：任何一个二进制数展开公式是：

D=Σki2i

注意：上式中的用到的2 和10 角标分别表示的是二进制（b）和十进制数。

判断一个数是不是二进制数，从两方面判断，第一前缀，二进制的前缀是0b 或者b 开头，第二就是看数值，数字只能是0 或者1。比如：0b1001、0b01101 等。(www.daowen.com)

3.八进制

对于八进制来讲，用的地方不是很多，通过对比前面介绍的两种进制来分析，那么八进制数的每一位就只能从0～7 中取一位，并且计数的基数是8，其中低位和相邻高位之间的运算关系遵守“逢八进一”，故称为八进制。任何一个八进制数可以按照十进制数展开为：

D=Σki8i

通过上式公式可以把一个八进制数计算与之等价的十进制数值，例如：

(12.4)8=1 x 81+2x 80+4 x 8−1=(10.5)10

其中式中的下脚标8 为八进制数，有的时候也用O 表示。

判断一个数是不是八进制，通过两部分，第一是前缀，八进制的前缀为O，第二就是看数值，每一位都在0～8 区间，比如：O157、O445 等。

4.十六进制

十六进制数的每一位有16 个不同的数码，分别用0～9、A（10）、B（11）、C（12）、D（13）、E（14）、F（15）表示。，并且计数的基数是16，其中低位和相邻高位之间的运算关系遵守“逢十六进一”，故称为十六进制。任何一个十六进制数可以按照十进制数展开为：

D=Σki16i

通过上式公式可以把一个十六进制数计算与之等价的十进制数值，例如：

(2A.7F)16=2 x 161+10x 160+7 x 16−1+15 x 16−2=(42.4960937)10

其中式中的下脚标16 为十六进制数，有的时候也用H 表示。

目前在微型计算机中普遍采用16 位、32 位、64 位二进制并行运算，而16 位、32 位、64 位的二进制可以用4 位、8 位、16 位的十六进制数进行表示，因而用十六进制符合书写程序十分方便，这在嵌入式开发领域得到了一个很好的体现。

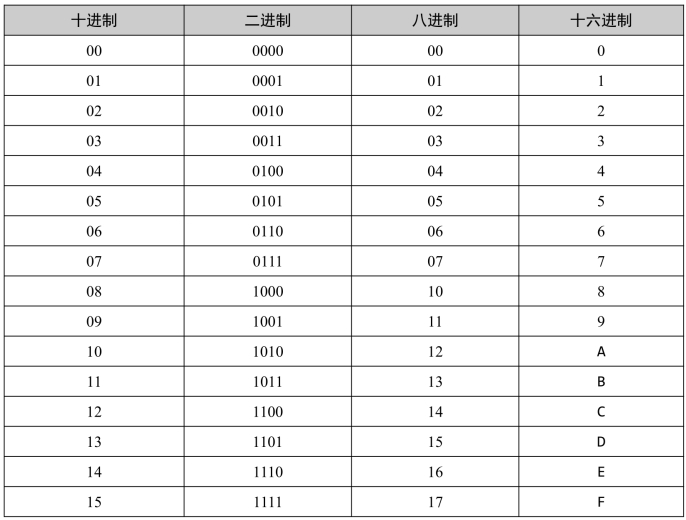
表1.1　不同进制的查找表