关于函数f的周期性。若T为非零常数，对于定义域内的任一x，使f（x）＝f（x+T）恒成立，则f（x）叫做周期函数，T叫做这个函数的一个周期。

关于圆外与圆内旋轮线的周期性，设定圆半径为R，动圆半径为r，我们发现：

（1）当半径之比R／r为有理数时，圆内（或外）旋轮线有周期性；

（2）当半径之比R／r为无理数时，圆内（或外）旋轮线没有周期性。

下面以圆外旋轮线为例予以证明，圆内旋轮线的证明与其类似。

证明思路：由图15（a）可见，若此圆外旋轮线有周期存在，则动圆上的定点P将回到初始位置，即动圆滚动了整数圈（记为b），且P经过了定圆的圈数也为整数（记为a）。此时有正整数a，b，使2πbr＝2πaR，即R／r＝b／a，从而R／r为有理数。这提示我们切点经过定圆的弧度为θ＝2aπ时，P将回到初始位置，呈现周期性。例如，在前面的图15（a）中，R＝3，r＝1，动圆滚动3圈时，P经过定圆1圈，回到初始位置，因此具有周期2π。严格证明如下。

证：若半径比R／r为有理数，则R／r必可表达为两互质的正整数之比p／q，因此当动圆滚动了p圈时，经过了定圆q圈，则T＝2qπ是旋轮线关于参数θ（切点经过定圆的弧度）的周期。这是因为：

当θ增加2qπ变为θ+2qπ，变为，相应增加了2（p+q）π，其正弦与余弦值都保持不变，因此

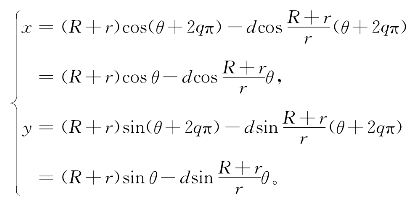
即T＝2qπ是旋轮线关于参数θ的周期。

当R／r为无理数时，由上面的分析可知，当周期存在时，R／r＝b／a必为有理数。因此，当R／r为无理数时，此时圆外旋轮线没有周期。

前面的图15（a）（R＝3，r＝1）与图15（b）（R＝3，r＝1或R＝5，r＝3），其图形直观佐证了此时的旋轮线有周期性。最后，我们取R＝，r＝1，d＝1，则R／r为无理数，利用数学软件Mathematica编程作图，分别绘制动圆绕经定圆内侧5周、50周、500周的圆内旋轮线，用以佐证此时的旋轮线没有周期性。程序代码如下：(www.daowen.com)

R＝Sqrt［2］；r＝1；d＝1；

ParametricPlot［｛（R－r）Cos［t］＋d Cos［（R－r）t／r］，

（R－r）Sin［t］－d Sin［（R－r）t／r］｝，｛t，0，10 Pi｝］

ParametricPlot［｛（R－r）Cos［t］＋d Cos［（R－r）t／r］，

（R－r）Sin［t］－d Sin［（R－r）t／r］｝，｛t，0，100 Pi｝］

ParametricPlot［｛（R－r）Cos［t］＋d Cos［（R－r）t／r］，

（R－r）Sin［t］－d Sin［（R－r）t／r］｝，｛t，0，1000 Pi｝］

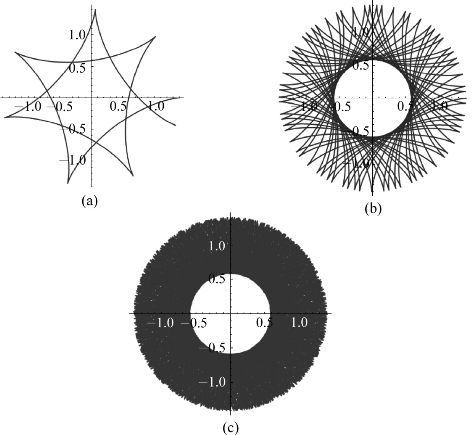
图20

图20（a），（b），（c）所示分别是动圆绕定圆内侧滚动5周（θ∈［0，10π］）、50周（θ∈［0，100π］）、500周（θ∈［0，1000π］）形成的内旋轮线的图像。由此可见，在动圆滚动500周内，无周期出现；随着滚动圈数的增加，旋轮线在一圆环区域上越来越密集。我们可以猜想，动圆无限滚动下去，旋轮线在此圆环区域越来越稠密。

旋轮线的应用，除了前面提到的两点间最速降线的经典案例外，在工业生产和高新技术领域有着更广泛的应用。