应用上，摆线（旋轮线）齿轮传动是由一对摆线齿轮组成的齿轮传动。圆内、圆外旋轮线常被用为齿轮轮廓线的一部分，以保证平滑的接触。摆线齿轮的齿廓由内摆线或外摆线组成。摆线齿轮传动分内（见图14（a））外（见图14（b））啮合和齿条啮合（见图14（c））3种。齿条的齿顶和齿根都是滚圆在直线上滚成的摆线。

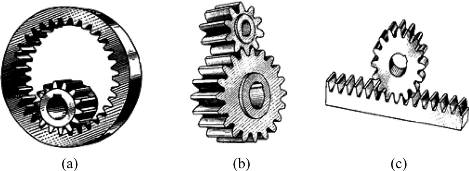
图14

如果让动圆沿着一个定圆滚动，而不是沿着直线滚动的话，我们将得到圆内旋轮线或圆外旋轮线。圆内或圆外旋轮线的定义如下：

（1）动圆沿着定圆的外侧滚动，动圆圆周上某定点形成的轨迹为圆外旋轮线（epicycloid），如图15（a）所示；

（2）动圆沿着定圆的内侧滚动，动圆圆周上某定点形成的轨迹为圆内旋轮线（hypocycloid），如图15（b）所示。

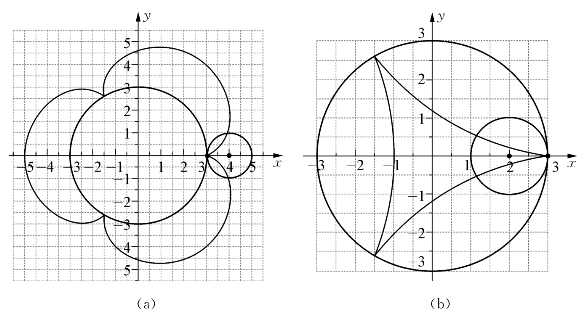
图15

（大圆为定圆，小圆为动圆，曲线为旋轮线）

更一般地，动圆上的定点可取在圆周上、圆内或圆外。定点在圆内的旋轮线称为短幅旋轮线（curtate cycloid），如图16（a）所示；定点在圆外的旋轮线称为长幅旋轮线（prolate cycloid），如图16（b）所示。

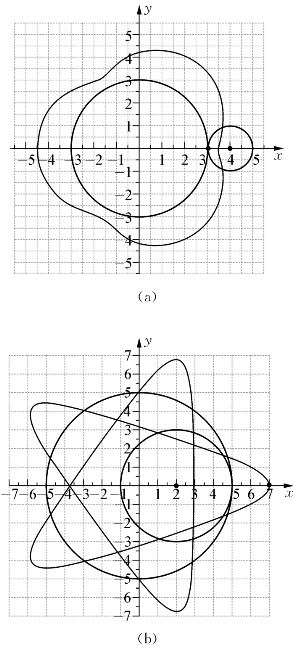
图16

（大圆为定圆，小圆为动圆，曲线为旋轮线）

在图14与图15中，大圆为定圆，小圆为动圆，曲线为旋轮线，动圆分别在圆外和圆内绕定圆转动，得到相应的圆外旋轮线与圆内旋轮线。

在日常生活与物理学中有很多旋轮线的例子。火车前进时，车轮边缘点的轨迹即为长幅旋轮线。从地球参考系看，行星的运动轨迹也近似为旋轮线。

设定圆半径为R，动圆半径为r。当动圆沿着定圆外侧滚动时，取初始切点P为动圆上的定点，以定圆圆心为原点O，以OP为x轴建立直角坐标系。设θ为切点经过定圆的弧度（即连接两圆心的线段与x轴的夹角），α为切点经过动圆的弧度（见图17）。由于切点在两圆上经过的距离相等，即θR＝αr，因此α＝θR／r。

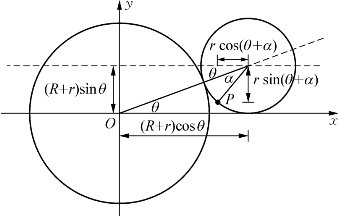(www.daowen.com)

图17

P的横坐标为（R+r）cosθ-r cos（θ+α），纵坐标为（R+r）sinθr sin（θ+α）。因此，圆外旋轮线的参数方程为

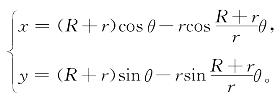
更一般地，设动圆上的定点（可在圆周上、圆内、圆外）到动圆的中心的距离是d，此时圆外旋轮线的参数方程相应为可类似求得动圆沿着定圆（R＞r）的内侧滚动得到的圆内旋轮线的参数方程为

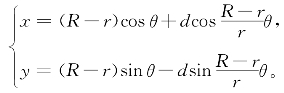
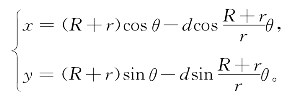
当d＝r时，定点在圆周上；当d＜r时，定点在圆内，相应的旋轮线为短幅旋轮线；当d＞r时，定点在圆外，对应的旋轮线为长幅旋轮线。我们观察一些有趣的例子：方程形式为的曲线，其中n为正实数。

讨论轨迹生成。假设有一个定圆，若有另一个半径是刚才圆形的1／（n－1）倍的圆在上滚动，则圆周上的一定点在滚动时划出的轨迹就是一条外摆线。

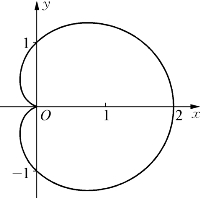
图18

心脏线是外摆线的一种，这时n＝2。心脏线的英文名称是“cardioid”，是卡斯提伦（de Castillon，生卒不详）在1741年的“Philosophical Transactions of the Royal Society”一文中发表的，意为“像心脏的”（见图18）。

取不同的n值，就可以得到精美的外摆线图。肾脏线亦是外摆线的一种，其n为3。图19所示分别是n＝3，9，1．3，e时的情况。

图19