1638年，伽利略在《论两种新科学》中以为最速降线是圆弧，后来人们发现这个答案是错误的。约翰·伯努利参考之前惠更斯分析过的等时降落轨迹，证明了最速降线是旋轮线，并在1696年6月在《博学通报》发表。

下面，我们利用简单有效的方法证明最速降线就是翻转的旋轮线。

在重力作用且忽略摩擦力的情况下，一个质点在一点A以速率为零开始，沿某条曲线到不高于A的一点B，沿怎样的曲线能令所需的时间最短呢？这就是“最速降线问题”，又称“最短时间问题”、“最速落径问题”。

“最速降线问题”的求解方法很多，通常的方法是利用变分法求解极值问题，这需要泛函分析和微分几何的高深知识。这里，我们只利用简单的物理知识和一点微积分基础，就可以证明这个较为复杂的问题。以下是我们的证明过程。

证：根据费马原理，两点间光线传播的路径是所需时间最少的路径。利用该原理，通过假设光在光速以恒定竖直加速度（也就是重力加速度g）加速的介质中运动形成的轨迹来导出最速降线。

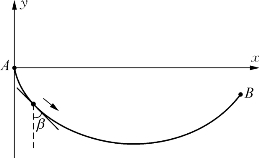
图11

设质点A的质量为m，我们以A的初始位置为坐标原点（0，0），重力方向为纵轴建立平面坐标系（见图11）。

假设质点某时刻的位置为（x，y），速度为v，速度方向与竖直方向的夹角为β。刚开始当质点A的速度为零时，夹角也必然是零，即初始β＝0，即最速降线在起始处与竖直方向相切。设质点下落竖直距离D后到最低点，达到最大速度，此时夹角β变为90°，则A的初始动能为0，势能为0，下落到最低点时，达到最大速度vD，则其动能为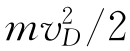，势能为－mgD，在位置（x，y）的动能为mv2／2，势能为mgy。运用机械能守恒定律，有

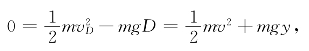
可得

由此可见点A下落到任意位置的速度与水平方向的位移（x）无关。根据光的折射定律，有

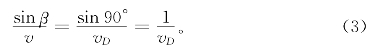(www.daowen.com)

由式（2）与式（3），得

下面求x关于夹角β的表达式，记d x为水平方向的路径微分，d s为运动方向的路径微分，有

由式（4）得d y＝-D sin（2β）dβ，代入式（5），得

由式（6）及初始条件β＝0时，x＝0，可知

联立式（4）与式（7）：

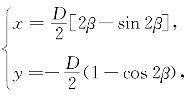
它与半径a＝D／2，参数θ＝2β的旋轮线方程

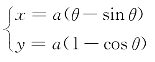
关于x轴对称。因此最速降线实际上是翻转的旋轮线的一段。