在中世纪航海时代，时间的掌握是关乎全船人生命安危的大事，想要和大海搏斗，时间是不可或缺的因素。古时候是以沙漏、水钟来计时，但这些计时工具相当不准确。为了增加船员生存的机会，发明精确的计时器变成当时科学界的当务之急，对时间更高的测量要求成为当时科学界的重要问题。

那时在意大利有一位年青科学家伽利略，有一次在比萨斜塔处意外地发现一个有趣的现象；教堂的吊灯来回摆动时，不管摆动的幅度大还是小，每摆动一次用的时间都相等。当时，他是以自己的心跳脉搏来计算时间的。他曾用自制的滴漏来重新做单摆的试验，结果证明了单摆摆动的时间与摆幅没有关系，只与单摆摆线的长度有关。

伽利略的发现振奋了科学界，可是不久便发现单摆的摆动周期也不完全相等。原来，伽利略的观察和实验还不够精确。实际上，摆的摆幅愈大，摆动周期就愈长，只不过这种周期的变化很小，所以，如果用这种摆来制作时钟，摆的振幅会因为摩擦和空气阻力而愈来愈小，时钟也因此愈走愈快。

1673年，荷兰科学家惠更斯（Christian Huygens，1629—1695）想要找出一条曲线，使钟摆沿着该曲线摆动时，摆动周期完全与摆幅无关。他们放弃了物理实验，纯粹往数学曲线上去研究，终于找到了这条曲线，这条曲线与最速降线的数学表达式一致，那时他们把这种曲线叫做“摆线”（见图9），也叫“等时曲线”。因此，最速降线、摆线、等时曲线与旋轮线是一致的。

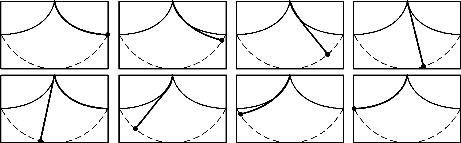
图9(www.daowen.com)

旋轮线的等时性性质，前面我们已经给出证明。

力学上摆线或旋轮线具有等时性质：当质点仅在重力作用下于摆线的不同位置沿摆线下滑，它们会同时到达底部。赫尔曼·麦尔维尔（Herman Melville）是19世纪美国最重要的小说家之一，他在名著《白鲸记》中对具有摆线（旋轮线）壁的“炼鲸油锅”（见图10）描述如下：对捕鲸船左舷的锅子，当用滑石打磨锅壁的时候，注意到这个神奇的现象，所有的东西无论从哪儿开始，都以同样的时间滑落到锅底。这就是旋轮线的一个性质。

图10