在无限集中，最基本的集合是可列集。所谓可列集，是指可以排成一列的无穷集合，换言之，就是可以与正整数集合一一对应的集合。

可列集是最小的无限集，因为从任意一个无限集中我们都可以逐次取出元素来，这个过程可以永远进行下去（请思考为什么这个过程不会终止），从而可以取出一个可列集。换言之，任何无限集都包含可列子集。

我们先介绍几个常见的无限集：N表示自然数集合；N＋表示正整数集合，Z表示整数集合，Q表示有理数集合，R表示实数集合。

显然，自然数集合N和正整数集合N＋都是可列集。

命题1：两个可列集之并是可列集（从而有限个可列集之并是可列集）。

证：设集合X＝｛x1，x2，x3，…，xn，…｝，集合Y＝｛y1，y2，y3，…，yn，…｝，则集合X∪Y可以表示为｛x1，y1，x2，y2，x3，y3，…，xn，yn，…｝，所以X∪Y是可列集。

由此可知整数集合Z是可列集，因为整数集合Z是自然数集合与负整数集合的并。

下面我们证明有理数集合Q是可列集。为证明集合Q可列，我们需要下述命题。

命题2：可列个可列集之并是可列集。

证：设对任意n∈N+，An是可列集，将An表示为

An＝｛xn1，xn2，xn3，…，xnk，…｝，

则（表示可列个集合之并）的元素全体可排成如图1所示的无穷方块阵：

图1

把所有这些元素排成一列的规则可以有许多，常用的一种称为对角线法则：从左上角开始，顺着逐条“对角线”（图1中箭头所示）将元素按从右上至左下的次序排列，也就是把所有的元素排列成

x11，x12，x21，x13，x22，x31，x14，x23，x32，x41，…，

这样的规则使无穷方块阵中的全部元素排成一列，而且保证不会遗漏一个元素。

命题3：有理数集合Q是可列集。

证：由于区间（-∞，+∞）可以表示为可列个区间（n，n+1］（n∈Z）的并，我们只需证明区间（0，1］中的有理数是可列集即可。

由于区间（0，1］中的有理数可唯一地表示为既约分数，其中p∈N+，q∈N+，q≤p，并且p，q互质，我们按下列方式排列这些有理数：

分母p＝1的既约分数只有一个，　x11＝1；

分母p＝2的既约分数也只有一个，　

分母p＝3的既约分数有两个，　

分母p＝4的既约分数也只有两个，　……

一般地，分母p＝n的既约分数至多不超过n-1个，可将它们记为xn1，xn2，…，xnk（n），其中k（n）≤n-1。

于是，区间（0，1］中的有理数全体可以排成

x11，x21，x31，x32，x41，x42，…，xn1，xn2，…，xnk（n），…。

这就证明了有理数集Q是可列集。

在集合论中还有一个概念称为“测度”，它反映了一个实数集合在数轴上所占据空间的大小，或者说是占据了多少“长度”。那么把所有的有理数排成一排，“长度”为多少呢？我们有下面的结论。

命题4：有理数集合Q的测度为零。

证：因为有理数集合是可列集，记r1，r2，r3，…，rn，…是全体有理数的一个排列，则对任意给定的ε＞0，取一列开区间I1，I2，I3，…，In，…，使得In的长度为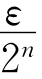，且rn∈In（n＝1，2，3，…），则开区间列I1，I2，I3，…，In，…盖住了全体有理数，而这列开区间的长度之和为ε。由于ε可以任意小，可知所有的有理数排成一排，“长度”（测度）为零。

素数集合

我们再来讨论一个正整数集合的子集，即素数集合

｛2，3，5，7，11，13，17，…｝。

素数是数论研究的重要内容，关于素数的规律，人类有许多猜想，至今还有不少猜想既没有被证明，也没有被否定，如哥德巴赫猜想，孪生素数问题等。数学家欧拉（Leonhcerd Euler，1707—1783）曾经说过：一直以来，数学家总是在孜孜不倦地寻找素数的规律，但是很难成功。我们可以把素数看作人类无法参透的奥秘。

通过分析，我们能够发现素数在正整数中的分布是很不规则的，而且随着正整数越来越大，素数的密度就越来越稀。下面我们问一个问题，是否正整数大到一定的程度，就没有素数了呢？答案是否定的。换言之，素数集合是无穷的（从而可知素数集合也是可列集）。关于这一命题，古希腊数学家欧几里得在他的《几何原本》中用反证法给出了一个漂亮的证明。

命题5：素数的个数无穷。

证：大于1的正整数包括素数与合数，素数只能被1与本身整除，合数是除了1与本身之外，至少还能被一个素数整除的数。如果素数有限，设它们的全体为p1，p2，…，pn。现构造一个数p1·p2·…·pn＋1，显然它比每个素数都大，而且它不能被任意一个素数整除，那么，它是素数还是合数呢？如果它是素数，则与素数全体为p1，p2，…，pn矛盾；如果它是合数，则因为它不能被任意一个素数整除，也产生矛盾。所以素数个数一定是无穷多个。

数学史上的第一次危机

公元前5世纪，古希腊毕达哥拉斯学派对数学有深入的研究，最著名的结果是关于直角三角形的毕达哥拉斯定理（又称为勾股定理）。该学派最基本的学说是“万物皆数”，即认为世界上一切事物都可归结为“数”，这里的“数”是指有理数。他们研究数学的出发点是“任何两条线段都是可公度的”。所谓“任何两条线段都是可公度的”，是指对任意两条长度为l1与l2的线段，一定存在长度为l的线段，使得l1＝ml，l2＝nl，其中m，n是正整数。这个命题等价于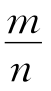＝，换言之，任意两条线段长度之比是有理数。但是后来毕达哥拉斯学派自己认识到这个命题是错误的，因为他们发现了正五边形的对角线与边长不可公度。为简单起见，下面我们证明正方形对角线与边长不可公度。

由勾股定理，正方形对角线长与边长之比是一个平方等于2的数，我们记它为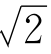。下面用反证法证明不是有理数。

命题6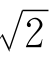：不是有理数。

证：采用反证法。假设，其中m，n互质，则可以得到n2＝2m2，即n是偶数；令n＝2k，则又可以得到m2＝2k2，即m也是偶数，与假设m，n互质矛盾，由此可知不是有理数。

数学家把不是有理数的数称为无理数，而把全体有理数和无理数合并在一起得到的集合称为实数集合，记为R。

“任何两条线段都是可公度的”这一错误命题，从根本上对毕达哥拉斯学派“万物皆数”学说形成冲击，从而导致数学史上的第一次危机。毕达哥拉斯学派是一个宗教形式的组织，他们极力掩盖事实，甚至想将公布这一事实的学者葬身海底。他们希望通过回避“任何两条线段都是可公度的”这一错误出发点来化解危机，但是这一危机不是局部的、表面的，而是全局的、本质的。这一危机直到19世纪实数理论建立以后才得到根本的解决。

实数集合R不可列

下面我们证明实数集合R的一个重要性质，即实数集合不可列。

命题7：实数集合R不可列。

证：我们只需要证明区间［0，1）中的实数是不可列的。先将区间［0，1）中的实数表示成无限小数，注意无限小数0．a1a2…ap 000…（ap≠0）与无限小数0．a1a2…（ap-1）999…是相等的。为了保持表示的唯一性，我们约定在无限小数表示中不出现后者。这样，区间［0，1）中的任何一个实数就可以由一个确定的无限小数来表示。

我们采用反证法。假设区间［0，1）中的实数可排列成x1，x2，…，xn，…，然后证明一定能找出区间［0，1）中的一个实数，它不在这个序列中，这就说明区间［0，1）中的实数太多了，无法排成一列。换言之，实数集合不可列。

设

x1＝0．a11a12a13a14…，

x2＝0．a21a22a23a24…，

x3＝0．a31a32a33a34…，(www.daowen.com)

……

xk＝0．ak1ak2ak3ak4…，

……

取b＝0．b1b2b3…bk…，0≤bi≤9，i＝1，2，3，…，其中b1≠a11（说明b≠x1），b2≠a22（说明b≠x2），b3≠a33（说明b≠x3），…，bk≠akk（说明b≠xk），…（只要求不把全部的bi都取为9），则b必在区间［0，1）中，但不在x1，x2，…，xn，…这个序列中。

上述方法称为康托（Georg Ferdinand Ludwig Philipp Cantor，1845—1918）对角线法。康托是德国数学家，是集合论的创始者。

有理数集合与实数集合的势

前面我们讲过，如果两个集合（的元素）之间能建立一一对应关系，则称这两个集合的“势”相等。有理数集合与可列集之间可以建立一一对应，所以它们的“势”相等；有理数集合与实数集合之间不能建立一一对应，它们的“势”不相等。

我们把可列集的势定义为“阿列夫零0”，把实数集的势定义为“阿列夫0与是希伯来文字）。所以有理数集合的势为“阿列夫零0”。由于无理数集合能与实数集合建立一一对应（见下面的例题3），无理数集合的势为“阿列夫”。

下面我们举例说明如何建立两个无限集之间的一一对应。

例题1：求实数集合（－1，1）与（－∞，＋∞）（即R）之间的一一对应。

解：函数y＝tan（x）的定义域为（-1，1），值域是（-∞，+∞），它是一个严格单调函数，所以它建立了（-1，1）与（-∞，+∞）之间的一一对应。

例题1说明区间（－1，1）中的实数与全体实数的个数一样多，所以区间（－1，1）中的实数全体的“势”也是“阿列夫”。

例题2：求开区间（0，1）与闭区间［0，1］中实数之间的一一对应。

解：要找如例题1的由初等函数建立的一一对应是不行的。我们采用如下方法：在开区间（0，1）中任取可列无穷多个数，记为x1，x2，x3，…，xn，…，然后让x1与0对应，x2与1对应，再让x3与x1对应，x4与x2对应，…，xn＋2与xn对应，…，一直对应下去。至于x1，x2，x3，…，xn，…以外的数，让它们自己与自己对应，这样我们就得到了开区间（0，1）与闭区间［0，1］实数之间的一一对应。

我们已经知道实数全体不可列，这一事实蕴含了无理数全体也是不可列的，也就是无理数全体与有理数全体之间不能建立一一对应。因为如果无理数全体可列，由于实数集合是无理数全体与有理数全体之并，就与实数集合不可列矛盾。

下面我们讨论实数全体与无理数全体是否可以建立一一对应。

例题3：求实数全体与无理数全体之间的一一对应。

解：我们已经知道有理数集合Q可列，设Q＝｛r1，r2，r3，…，rn，…｝。

在无理数集合中任取一个可列子集X＝｛x1，x2，x3，…，xn，…｝，则Q∪X也是可列集，于是可以构造集合X与集合Q∪X之间一一对应，而至于Q∪X以外的数，则让它们自己与自己对应，这样我们就得到了实数全体与无理数全体之间的一个一一对应。由此可知无理数集合的“势”也是“阿列夫”。

代数数与超越数

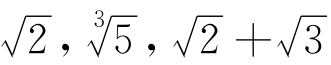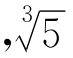我们已经知道，有理数之外还有无理数，如，等等，我们还知道是代数方程x2-2＝0的解是代数方程x3-5＝0的解是代数方程（x2-5）2＝24的解（因为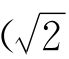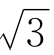（+）2-5）2＝24）。由此容易想到，如果构造一个集合，把所有这些整系数代数方程的解都包含进来，是否就能得到实数全体了呢？

我们称

anxn+an-1xn-1+…+a0＝0

为n次整系数代数方程，其中方程的系数a0，a1，a2，…an为整数，且没有公因子。整系数代数方程的解称为代数数。

代数数全体包含有理数全体，因为是代数方程mx-n＝0的解。

显然代数数集合比有理数集合大得多，于是就有以下的问题：代数数集合是否与实数集合的“势”一样呢？答案又是否定的。

命题8：代数数可列。

证：定义整系数代数方程anxn+an-1xn-1+…+a0＝0的“高度”为

h＝（n-1）+|an|+|an-1|+…+|a0|，

则高度为1的代数方程只有1个x＝0；高度为2的代数方程只有x±1＝0，2x＝0，x2＝0等4个；依此类推，高度固定的代数方程只有有限个，而每个代数方程的解也只有有限个，所以高度固定的代数方程的解为有限集。由于可列个可列集之并是可列集，可列个有限集之并必定是可列集，由此可知代数数集合也是可列集，此结果由德国数学家康托（Georg Ferdinand Ludwing Philipp Cantor，1845—1918）于1874年得到。

非代数数的实数称为超越数。由于代数数可列，可知超越数是不可列集，它的势大于可列集的势！关于有理数、代数数与超越数，有数学家做了如下的描述：如果把实数比喻为茫茫夜空，则有理数（或代数数）就如同茫茫夜空中的星星！

如果用刀去切数轴，在下面的意义下，我们称切到有理数（或代数数）的概率是零：设用刀去切数轴n次，用切到有理数（或代数数）的次数除以n，当n趋于无穷大时，该商的极限为0。

数学家寻找超越数的历史

数学家从理论上证明了超越数的存在，而且知道超越数比代数数多得多，但是对超越数的了解却非常少，而且寻找超越数的过程非常困难。

1851年，法国数学家刘维尔（Joseph Liouville，1809—1882）首先找到了一个超越数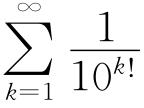：；1873年，法国数学家埃米特（Charles Hermite，1822—1901）证明了自然对数的底数e是超越数；后来，在埃米特工作的基础上，数学家陆续得到了以下一系列结果：

设a≠0是实的代数数，则ea是超越数。该结论包含了e是超越数。后来又进一步得到：设a≠0是复的代数数，则ea也是超越数（即不是整系数代数方程的解）。由于＝1，可知π也是超越数，这一结果是由德国数学家林德曼（Carl Louis Lindemann，1852—1939）于1882年得到的。

进一步的结果还有：

设a≠0，1是代数数，b是代数无理数，则ab是超越数；

若椭圆的长、短半轴是代数数，则椭圆的周长是超越数；

双纽线（x2+y2）2＝2（x2-y2）的周长是超越数；

区域的面积是超越数，其中α，β是非整数有理数；

连分数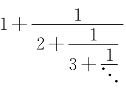是超越数，等等。

化圆为方问题

化圆为方问题是古希腊著名的初等几何三大世界难题之一，要解决这一问题，需要对给定的单位长度的线段，利用圆规与直尺作出长度为的线段。但是数学家发现，可以用圆规与直尺作出的线段，其长度只能是自然数经过有限次加、减、乘、除与开平方所得到的数。换言之，可以用圆规与直尺作出的线段长度，必定是某个整系数代数方程的解。既然π不是代数数，而是超越数，从而也是超越数，它不可能是某个整系数代数方程的解，因此化圆为方问题是不能用直尺与圆规解决的。这个问题从提出到解决，数学家花了2300多年的时间。

一个特殊的集合——康托集

最后我们介绍在集合论中一个非常著名的集合，称为康托集，它的测度为零，但它与实数集合的“势”相等。

我们采取挖掉“三分中段”的方法（即三等分后挖掉中间一段）：先从闭区间［0，1］中挖掉开区间，再从余下的闭区间中挖掉开区间，然后再从余下的闭区间中挖掉开区间，这个过程可以一直进行下去，最后留下来的集合称为康托集。

首先，康托集不是空集，因为至少上面所有区间的端点都是属于康托集的。

其次，从［0，1］闭区间中挖走的一列开区间的长度之和为

由此可知康托集的测度为零。

最后我们说明康托集与［0，1］区间上实数集合的“势”相等。可以这样来看：把［0，1］区间中的数写成三进制的小数，则第一次挖掉区间，相当于把三进制小数第一位是1的数全挖掉了；第二次挖掉区间，相当于把三进制小数第二位是1的数全挖掉了；第三次挖掉区间和，相当于把三进制小数第三位是1的数全挖掉了；依此类推，我们得到康托集就是三进制小数表示中只出现0与2两个数字的点集。如果我们把［0，1］区间上实数全体写成二进制小数，就容易理解康托集与［0，1］区间上的实数集合是一一对应的，所以它们的“势”相等。

复旦大学数学科学学院　陈纪修