【摘要】：如图14所示，有两个具有相同底面半径R的圆柱体，设它们的（中心）轴相交，且交角为直角，求这两个圆柱体公共部分的体积。但这没有关系，我们采用如下的方法：作一张平面经过两圆柱体相交的轴，称这张平面为轴平面，它把物体分成前后相等的两半。过两轴交点作轴平面的垂直线，则其包含在前一半物体内的部分长为R。
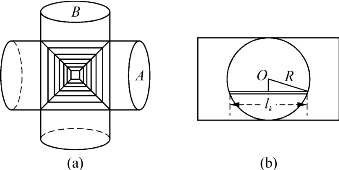
图14
最后我们来解一个难一些的问题。如图14所示，有两个具有相同底面半径R的圆柱体（分别记为A与B），设它们的（中心）轴相交，且交角为直角，求这两个圆柱体公共部分的体积。
问题的难处在于所研究的物体形状比较复杂，不容易清楚地表示出来。但这没有关系，我们采用如下的方法：作一张平面经过两圆柱体相交的轴，称这张平面为轴平面，它把物体分成前后相等的两半。我们只需要求前一半的体积。
任意作一张平面平行于轴平面，要求与轴平面的距离小于R，则它与圆柱体A的截口是一条横的平行带，与圆柱体B的截口是一条垂直的平行带，两条带的公共部分是一个正方形，由此可知该平面与物体的截口是一个正方形，而且当该平面与轴平面的距离增加时，两条带的宽度就减小，从而正方形的边长也减小（见图14（a））。知道了这一点，问题就不难解了。过两轴交点作轴平面的垂直线，则其包含在前一半物体内的部分长为R。将该线段n等分，过各个分点作平行于轴平面的平面，将物体分成n层。图14（b）所示就是从顶上看下来所讨论的物体的形状。我们近似地将每一层看成底面为正方形的柱体（这自然是不精确的，但当n很大时，误差可以忽略不计）。记lk为从后往前数第k层柱体的底面正方形的边长，则lk＝
，于是第k层柱体的体积为
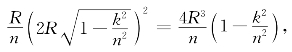
因此前一半物体的近似体积为(www.daowen.com)
要得到前一半物体的精确体积，只要令n→∞，于是得到
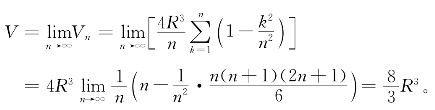
所以整个物体的体积是
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
