一副扑克除去大小王，有52张，共4种花色：黑桃、红桃、梅花和方块，每种花色13张牌，分别是A，1，2，3，4，5，6，7，8，9，10，J，Q，K。下面计算从52张牌任取5张所得各种组合（牌型）的概率。

（1）“同花顺”（straight flush）。同一种花色按顺序连续5张组成的牌型称为“同花顺”（见图1）。

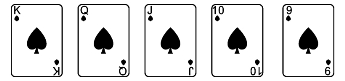
图1

特别是由同一花色的A，K，Q，J，10组成的“同花顺”称为“同花大顺”（royal Flush），在香港称为“黄袍旗”（见图2）。

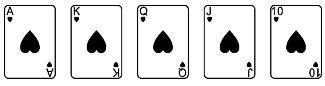
图2

A也可以和2，3，4，5组成“同花顺”（见图3），这是方块中最小的“同花顺”。但A不能在中间，如图4所示不是“同花顺”。

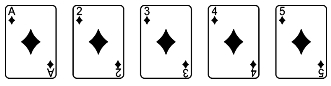
图3

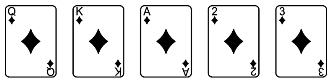
图4

由上可知，构成“同花顺”的牌型有：

A2345，23456，…，10JQKA共10种，共有4种花色，所以出现“同花顺”的概率为

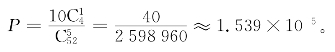
其中出现“同花大顺”的概率为

除去“同花大顺”的“同花顺”出现的概率为

（2）“四条”（four of a kind）。4张同一点数加上一张其他牌，这种牌型称为“四条”，也称为“铁支”、“炸弹”等，如图5所示。

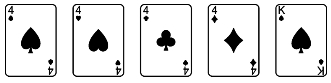
图5

一共有13种不同的点数，所以出现“四条”的概率为

（3）“满堂红”（full house）。3张相同点数的牌，加上2张有相同点数的其他牌组成的牌型称为“满堂红”，也称为“俘虏”、“葫芦”、“骷髅”等，如图6所示。

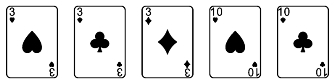
图6

作为3张相同点数的牌的点数有13种选择，且在4种花色里可任意取3种花色，作为另外2张相同点数的牌的点数有剩下的12种选择，且4种花色可任选2种，所以，出现“满堂红”的概率为

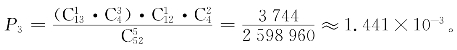
（4）“同花”（flush）。5张牌同一花色的牌型（“同花顺”除外）称为“同花”，如图7所示。

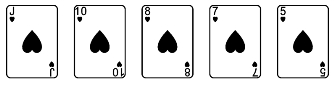
图7

这里指的“同花”是除去“同花顺”的情形，因此，此牌型出现的概率计算如下：花色有4种情况，每一种花色在13张牌中任取5张，然后再减去同花顺牌型的40种情况，即有

（5）“顺子”（straight）。按顺序连续的5个点数牌型称为“顺子”，即在“同花顺”中5张牌不是同一种花色的情况。5张顺连的牌型有10种，每张可以有4种花色，减去5张花色相同的4种，即为顺子的总基本事件数，于是出现顺子的概率为(www.daowen.com)

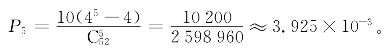
（6）“三条”（three of a kind）。5张牌有3张牌点数相同，其余2张牌和这3张牌的点数不同，这2张牌的点数也不相同，这样的牌型称为“三条”，如图8所示。

3张牌同点数有13种选择，其在4种花色里任选3种，然后在

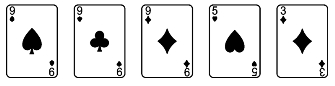
图8

12种点数里选出2种作为其余2张牌且花色可任意，因此，出现“三条”的概率为

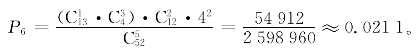
（7）“两对”（two pairs）。2张相同点数的牌，加另外2张相同点数（点数和前2张不同），再加1张与前面点数都不同的牌组成的牌型称为“两对”，如图9所示。

图9

在13种点数中可任选2个点数作为“对子”（两张点数相同的牌）的点数，其花色可任选2种，然后在11种点数中选1种且花色任意作为其余的1张牌，因此“两对”出现的概率为

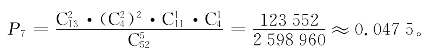
（8）“一对”（one pair）。5张牌里有且仅有2张牌点数相同，其他牌之间点数互不相同的牌型称为“一对”，如图10所示。

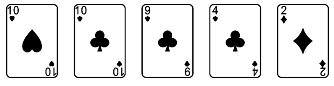
图10

“对子”的点数有13种选择且在4种花色里任选2种，然后在剩下的12种点数中任选3种，花色任意，因此，“一对”出现的概率为

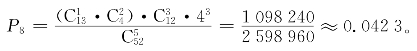
（9）“无对”（no pair）。除了以上牌型以外的牌型称为“无对”。“无对”牌是既不能构成“顺子”也不能构成“同花”且点数各不相同的牌型，如图11所示。

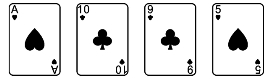
图11

所以，“无对”出现的概率为

或者直接计算：在13种点数中任取5种减去10种构成顺子的情况，花色任意但要减去4种花色相同的情况，因此所求概率为

根据越难出现（即出现可能性越小）的牌型越大的原则，德州扑克游戏中牌型的大小顺序为

“同花顺”＞“四条”＞“满堂红”＞“同花”＞“顺子”

＞“三条”＞“两对”＞“一对”＞“无对”。

如果牌型一样，则利用数字和花色决定胜负，其中数字优先，数字和花色大小顺序为

A＞K＞Q＞J＞10＞9＞8＞7＞6＞5＞4＞3＞2；

黑桃＞红桃＞梅花＞方块。

但在“顺子”5，4，3，2，A中，A是最小的一点。

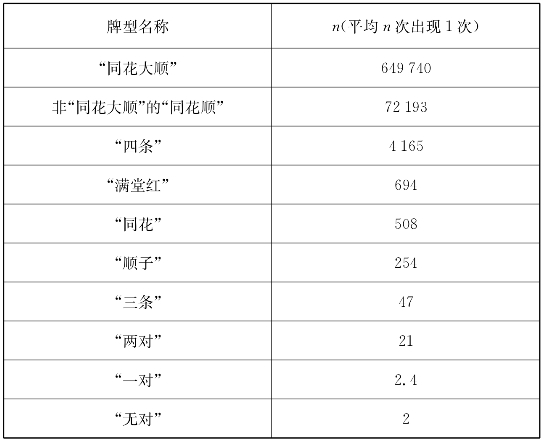
表1中列出了大约平均多少次会出现1次相应的牌型，例如，表1中右边第一个数表示平均649740次才出现1次“同花大顺”，等等。

表1