一个随机试验在相同条件下进行了n次试验，若事件A共发生了m次，我们称比值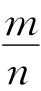为事件A发生的频率。所以，频率的大小表示事件A发生的频繁程度，也体现了事件A发生的可能性大小。但是同样进行几次试验，事件A发生的频率一般是不同的。例如，抛硬币100次，第一次做“正面次数”可能出现51次，第二次做“正面次数”可能出现46次。读者无妨去试一试，当试验次数n越小时，频率越不稳定；当n越来越大时，频率逐渐稳定于某个常数，这个频率的稳定性也就是统计规律性。因此我们若用这个频率的稳定值来表示事件发生的可能性大小应该是合适的。

概率就是度量一个事件发生的可能性大小的数值，数学中为了理论研究等需要对概率作出抽象的定义，这里不作详细介绍。当试验次数不断增加，事件A发生的频率的极限值（稳定值）即为事件A的概率，记为P（A），概率有以下基本性质：

（i）对任意事件A，P（A）≥0；

（ii）若样本空间记为S，则P（S）＝1；

（iii）若事件A1，A2，…，An两两不可能同时发生，则A1，A2，…，An中至少有一个事件发生的概率

P（A1∪A2∪…An）＝P（A1）+P（A2）+…+P（An）。(www.daowen.com)

若A，B两个事件不可能同时发生，且A，B中必有一个发生，则称B为A的对立事件（也称逆事件），记为B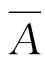＝；或者A为B的对立事件，即A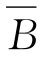＝。也就是有A∪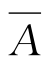＝S（样本空间），显然，

对两个事件A和B，至少有一个发生的概率

P（A∪B）＝P（A）+P（B）-P（A∩B），

其中P（A∩B）表示A，B同时发生的概率。