意大利学者伽利略在观察教堂内挂灯的摆动时，发现挂灯摆动的周期与摆动的幅度似乎是无关的，这使得伽利略想到，可以利用摆动的物体来调节钟表的走动。后来人们发现，伽利略的观察并不精确，事实上，摆的摆幅越大，摆动的周期就越大。由于有空气的阻力，摆动的幅度会逐渐减小，周期也会逐渐减少。注意伽利略考虑的摆的摆锤（或摆的重心）是在一个圆周上运动的，我们把这种摆称为圆周摆。

既然圆周摆的周期与摆幅有关，荷兰学者惠更斯（Christiaan Huygens，1629—1695）就想找一种曲线，使得摆的重心在这种曲线上运动时，摆动的周期与摆幅没有关系。惠更斯把这种曲线称为“陶塔赫隆娜”（希腊文“等时”的意思）曲线。他取得了成功，这种曲线不是别的，正是前面讨论过的旋轮线！不过它的位置是倒转过来的。

图10所示是一条倒转过来的旋轮线ABA′，设母圆的半径是R，则对称轴BB′的长度为2R。我们已经知道，将一小球挪到点A放手，由于重力的作用，小球会沿着旋轮线ABA′下滑到点B，而且所用的时间最少。旋轮线还有一个奇妙的性质：将小球挪到旋轮线上任意一点P0放手，小球同样会沿着旋轮线下滑到点B，且所用的时间与在点A放手、让小球沿着旋轮线下滑到点B的时间是一样的。也就是说，所用的时间与点P0的高度无关！下面我们来证明这一点。

图10

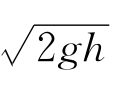设在点P0将小球放手，小球沿着旋轮线下滑到点P，设点P与点P0的高度差为h。我们先来求小球在点P时垂直向下的速度分量。首先小球在点P的速度可以由牛顿定理得到，即由mgh得到v＝，且速度的方向就是旋轮线的切线方向。记速度方向与垂直向下方向的夹角为φ，则小球在点P时垂直向下的速度分量为·cosφ。(www.daowen.com)

过点P0作水平线与对称轴BB′交于点D0，以BD0为直径作辅助圆，圆心为O′，半径记为r。再过点P作水平线，与对称轴BB′交于点D，与辅助圆交于点C，与以BB′为直径的母圆交于点T。记∠DO′C＝θ。由于旋轮线过点P的切线过母圆的顶点，可知∠TBB′＝φ。现在我们考虑一动点从辅助圆的顶点D0出发，以均匀的角速度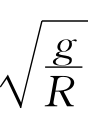沿辅助圆的圆周向下运动，则当该动点运动到与点P同一水平线上的点C时，该动点向下的速度分量为

这与上面求出的小球在点P时垂直向下的速度分量完全相同。

现考虑两个运动。第一个是小球从点P0开始沿旋轮线下滑，第二个是从辅助圆的顶点D0（与点P0同样高度）开始沿辅助圆周做匀速圆周运动，角速度为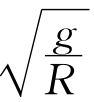。它们在运动过程中垂直向下的速度始终是相同的，所以它们到达旋轮线底部点B的时间应该是相同的。而第二个运动因为是匀速圆周运动，它需要的时间是可计算的，就是π，所以将小球挪到旋轮线上任意一点P0放手，小球沿着旋轮线下滑到点B所用的时间就是π，它与点P0的高度没有关系。由此我们知道，如果让一个小球在倒置的旋轮线形状的槽内来回滚动，开始的时候滚动的幅度可以很大，但是由于摩擦力的原因，滚动幅度会逐渐减小，但是滚动的周期不会改变。换个说法，如果一个摆的摆锤在一条旋轮线上运动，则它的摆动周期就与摆幅无关。按照上面的计算，我们知道摆动周期为4π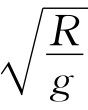，其中R是旋轮线母圆的半径。接下来我们面临的问题，就是如何使一个摆的摆锤在一条旋轮线上运动！