在我们所生活的这个宇宙之外，上帝创造了一个与我们的宇宙完全不同的宇宙。在这个宇宙中，也有一个充满生机的世界，与我们不同的是，这个世界的人们都生活在一个星盘上——一个在我们看来大小有限的圆盘，我们把这个圆盘称为庞加莱星盘，这样一个世界称为庞加莱世界。

生活在庞加莱星盘上的人们（包括一切生灵物体）都有一个非常奇特的特点：从我们的角度看，这些庞加莱人的大小随他们在星盘上所处的位置而变化。当他们在星盘的中心位置时，他们身材比较高大，但当他们向星盘的边缘移动时，他们的身材会变小，其身材的大小差不多与他们到星盘边缘的距离成正比。这样，他们越靠近边缘其身材越小，当他们趋向于边缘时，他们的身材大小也趋向于零。当然，这是从我们的角度去看他们，他们自己却感觉不到自己的身材大小会有什么变化，他们认为到哪儿自己的大小都一样。

荷兰艺术家埃舍尔（Macerits Coruelis Escher）曾经用其神奇之笔画了多幅名为“圆的极限”的画，很好地阐述了庞加莱的世界，其中一幅画叫做“天使与魔鬼”（见图1）。在这幅画中，埃舍尔用大大小小的白色天使和黑色魔鬼填满了一个圆，中间的天使和魔鬼比较大，越靠近边缘的天使和魔鬼越小，直至小到看不见。不过这个圆盘描述的是庞加莱世界，对这些天使和魔鬼本身来说，所有的天使和魔鬼都是一样大小，是完全平等的。他们并不觉得中间的天使比边上的天使更大、更高贵。同样，中间的魔鬼也并不比边上的魔鬼更大、更强壮。

图1

那么，在庞加莱的世界里，他们的生活会是怎样的呢？

尽管在我们看来，庞加莱星盘是一个有限的圆盘，但对于庞加莱世界里的人们来说，他们觉得生活在一个无限的世界中。如果他们向星盘的边缘走动，越靠近边界，身材会变得越小，步伐也会变得越短，这样他们会越走越慢，永远走不到星盘的边界。

按照庞加莱世界的特性，庞加莱人的身高和他们所处位置到星盘边界的距离大约成正比，从而他们的步伐长短也与到边界的距离成正比。不妨假设他们向边界走一步的大小是他们所在位置到边界距离的一半。如果一开始一个庞加莱人处于到边界距离为d的位置，向边界方向走去，则第一步步长为d／2，此时他到边界的距离是d／2，因而第二步步长为d／4，到边界的距离也为d／4，依此下去，n步以后走过的路程为d／2+d／4+…+d／2n＜d。只要步数n有限，走过的路程永远小于d。如果一直走下去，只会越来越靠近边界而到不了边界。

因此，这个我们看来有限的圆盘（庞加莱星盘）对庞加莱人来说，是一个永远达不到边界的无限世界，就像我们觉得我们的世界可以无限延伸，没有边界一样。这样，圆盘内的一条连接圆盘边界上两个点的线，对庞加莱世界的人们而言，是一条无限长的没有尽头的线。

现在看看如果庞加莱世界的人们要从一个地方走到另一个地方，他们会怎么走？假设一个庞加莱人从星盘的中心出发走向某个地方，毫无疑问，他会沿直线向那个地方进发，尽管他会越走越慢，也不会绕着走，这是最经济的走法。但是，如果从一个靠近边缘的地方走向另一个靠近边缘的地方，他还会沿直线走吗？很有可能这两个地方的连线会整个都很靠近边缘（如图2中的直线所示），比如两地不是太远但离边缘非常近。由于庞加莱人在星盘的边缘处会变得很小，步伐也会很小，如果他沿着直线走，就会走得非常慢，不远的两地在他们看来也会觉得很远。要走得快一点，他会先向星盘的中心拐一下，沿一条向中心方向弯曲的弧线走到目的地（如图2中虚弧线所示）。这是由于如果向中心靠一下的话，他的身材会变大，步伐也会变大，走得就更快一点，尽管弧线看上去似乎比直线要长一些，但实际走的步数更少。也就是说，对庞加莱人来说，走弧线比走直线更短、更经济。如果将两点间的最短线定义为“直线段”的话，那么，在庞加莱星盘上，庞加莱人的“直线段”不是我们认为的线段，而是向中心弯曲的弧线段。再将这样的“直线段”两端延伸到星盘的边缘，就得到庞加莱星盘上的“直线”。正如前面所说，这样的“直线”是无限长的。

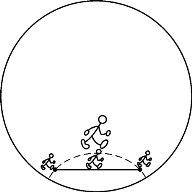
图2

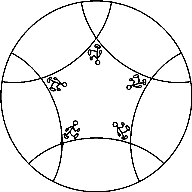
图3

在我们的世界里，如果我们沿直线走一段距离，在做3次左转90°并走同样长的距离，就会回到原来出发的地方，即我们沿正方形的边走了一周后会回到起点。但是在庞加莱星盘上，如果庞加莱人做同样的事，他们是回不到原来的出发地的。而如果他们做4次左转90°并走同样长的距离，倒有可能回到出发地（见图3）。奇特的庞加莱世界！

上面所说的庞加莱世界，是法国数学家、被誉为数学界最后一个全才的数学大师——庞加莱（Jules Henri Poincaré，1854—1912）为罗巴切夫斯基（Nikolas Lvanovich Lobachevsky，1792—1856）的非欧几何所构造的一个数学模型，称为庞加莱圆盘模型。庞加莱认为罗氏非欧几何可以在一个圆盘上实现，只要在这个圆盘上把两点间的距离做一下修改。设这个圆盘是笛卡尔直角坐标系Oxy中的单位圆D，即D＝｛（x，y）：x2+y2＜1｝，在D中的点p＝（x，y）处很小一段线的非欧长度Δhp和我们熟知的欧氏长度Δp之间满足如下关系：

(www.daowen.com)

这里||p||＝表示点p到圆盘D的圆心O的距离。如果非欧长度Δhp不变，当p向圆盘D的边缘靠近时，欧氏长度Δp将变小，并越来越接近于0，并且当||p||很接近1时，Δp≈2（1-||p||）Δhp，即正比于p到圆盘D的边界的距离，正如我们在庞加莱星盘中看到的那样。上面的Δhp是充分小的一段非欧长度，对圆盘D中任意两点p，q间的非欧距离，可以计算（需要用到微积分）得到

其中

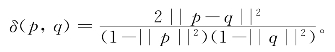
在这样的非欧距离下，圆盘D中的非欧“直线”就是那些和单位圆周x2+y2＝1垂直的圆弧（如图4中的每一条圆弧）。正如前面所述，这些圆弧不是有限长的，而是无限长的“直线”。

下面通过几个例子来说明这个圆盘上的几何实现了罗氏非欧几何。罗氏非欧几何的主要假设是用如下非欧平行公设替代了欧氏几何的平行公设，即非欧平行公设：过给定直线外一点可以作多于一条直线和给定直线平行。在这里，两条直线平行是指这两条直线互不相交。

在图4中，圆弧l是一条非欧“直线”，过点p的3条圆弧l1，l2，l3也都是非欧“直线”，我们看到这些“直线”都与“直线”l不相交，因此都是l的平行线，即过点p与“直线”l平行的直线有不止一条，事实上可以有无穷多条，见图5。

非欧几何的另一重要事实是三角形内角之和小于180°。这在图6中立即可以看到。读者也可以通过庞加莱的圆盘模型找到更多的非欧几何性质，比如非欧几何中不存在矩形，即4个角都等于90°的四边形。读者不妨自己试试看。

图4

图5

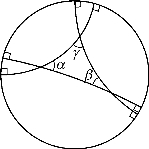
图6

复旦大学数学科学学院　邱维元