在《芥子须弥——圆周率π的秘密》(以下简称《π的秘密》)中讲到,超越数比代数数多得多。实数几乎全部都是超越数。这里我们希望证明,实数几乎全部都满足:写成无限小数以后包含任何的整数。也就是说在《π的秘密》中定义的超越数也几乎占据了实数中的全部。
首先我们证明,一个无限小数中不出现0到9中的一个(譬如0)的集合是一个零测集,即把它们放在一起,其长度为零。
把(0,1)区间10等分,再10等分,如此一直等分下去。那么在小数点后第一位出现0的数在第一次等分区间的第一个区间,我们把这个区间挖去,记得挖去1的1/10长度。剩下的9个区间第一位均不是0,其中第二位出现0的是这些已经10等分后再10等分的第一个区间,我们再把这些区间也挖去。这时挖去了9个1/10长度中的1/10,即9/10乘以1/10的长度。继续到n步,我们将要从长度是9/10的n次方中再挖去1/10。这样继续做下去,我们去掉所有在某处出现0的数,其总长度如下:关于9/10的n次方求和,再除以10。容易得到结果是1。也就是说,剩下的在小数中永远不出现0的这些点的集合的测度(长度)为零。数学中称为零测集。零测集意味着我们可以用一个一个小区间将这些点“盖”起来,而这些覆盖小区间的总长度可以任意小。
另外一种计算步骤如下:利用数学公式,记第n步要挖去的区间长度为an,已经挖去的总长度为sn,即sn=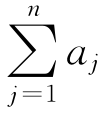 ,那么挖去的是(1-sn)/10=an+1,an应该趋于0,所以sn应该趋于1。
,那么挖去的是(1-sn)/10=an+1,an应该趋于0,所以sn应该趋于1。
我们可以把小数中不出现0的数的全体的集合记成N0,把不出现n的记成Nn。反之,将出现0的记成Y0,出现n的记成Yn。那么刚才我们已经证明N0的长度或测度为0,Y0的长度或测度为1。在(0,1)区间任意取一点,那么这点落在N0的概率为0,而落在Y0的概率为1。反之,如果有(0,1)区间某集合,在(0,1)区间任意取点,落在该集合的概率为p,那么这个集合的测度或者长度应该为p。
在《π的秘密》中提到:一个随机地一位一位写出来的,或者说均匀分布随机产生的无限位小数,它不包含整数n的概率为0。所以Nn的测度也为0,当然Yn的测度也为1。
对这个集合Nn,我们可以找到一个总长度为2的n次方分之ε的小区间族把它覆盖起来。这样我们找到了一个总长度小于2ε的小区间族把所有的Nn覆盖起来。而ε是可以任意选的,或者说我们可以让它越来越小,趋于无限小,那么我们得到:所有Nn的集合的并集的测度为0;反之,所有Yn的集合的交集的测度为1。
定理:在(0,1)区间任意取一点,它对应的实数展开的无限位小数表示中,包含任意整数n的概率为1。用数学符号表示为∩Yn的测度或长度为1。通俗地讲,在区间(0,1)中,几乎都是《π的秘密》中定义的超越数。
问题:是否所有的超越数都是《π的秘密》中定义的超越数?我们基本认为不是。这是基于猜想:两进制数0.1001000100001000001000000100000001…应该是超越数。这里0的添加是按正整数的增长添加的。这个猜想也有可能不对,好像太有规律了。但我们还可以猜想:按素数增长的添加应该是超越数,或者至少0的个数是以n!增长的,应该是超越数。但这个数不包含11,111等。
问题:(作为习题)如果在每一位0到9的添加时,概率不都是1/10,譬如j出现的概率是pj,而∑pj=1。那么上面的结论是否成立?(www.daowen.com)
回答:成立。
问题:上面将实数与(0,1)区间的点对应起来,实数用小数展开后第n个为j时,是在n-1次10等分后再10等分的第j段中。这是数学的一个基本方法,就是将代数中的数与几何上的点建立了联系。那么,在上一个问题中,当每次0到9中的数k是以概率Pk添加时,如何构造相应的几何模型?(提示:上面的模型使用区间的长度,现在可以构造函数,然后用函数下方的面积构造模型。)
问题:(作为习题)上面的讨论是针对十进制的小数,对两进制或其他任意进制是否成立?
这里要说一句,已经知道答案的习题不重要,当然可以用来训练自己。重要的是给出问题与问题可能答案的猜想,更为重要的是你自己给出新问题与新猜想。不要忘了,这个问题的基本猜想是π是《π的秘密》中定义的超越数。当然e可能也是。
进一步的问题:是否有些代数数也是超越数?譬如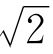 。那么,上帝就可以拿一个譬如正方形来创造世界了。
。那么,上帝就可以拿一个譬如正方形来创造世界了。
进一步的问题:如果π是超越数,那么在N位时可能已经出现了Nn个n。当N趋于无穷大时,Nn是否趋于无穷大?Nn/N趋于什么?这个问题就涉及更加哲学或宗教的问题:如果宇宙寂灭了,是否还会凤凰涅槃?是否还会有多次涅槃?涅槃的频率是多少?当然这是基于假设上帝是用圆来创造世界的。
复旦大学数学科学学院 吴宗敏
(本文摘自《数学文化》2015年第4期,此处文字略有改动。)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





