有一个激发学生智力的测试题目可能大家都已知道。老师拿了5顶帽子——3顶白帽子和2顶黑帽子——给3个聪明的学生看，然后他让学生们闭上眼睛，在每人头上戴上一顶白帽子，并将2顶黑帽子藏起来。每个学生只能看到另外两个学生头上的帽子，看不到自己头上的帽子。问学生们能否猜出自己头上帽子的颜色？据说，这个问题是华罗庚先生在爱因斯坦提出的问题的基础上经过改进后提出的，也称为“华罗庚帽子问题”。

初一看问题似乎无解，每个学生看到另外两个学生戴的是白帽子，那么自己戴的可能是剩下的1顶白帽子和2顶黑帽子中的一个，无法确定自己头上帽子的颜色，因此他们都犹豫了。但这是3个非常聪明的学生，不一会儿，他们不约而同地举手告诉老师猜到了自己头上所戴帽子的颜色。他们是怎么做到的呢？假设3位学生是甲、乙、丙，学生甲假想自己头上戴的是黑帽子，那么学生乙将看到1黑1白两种颜色的帽子，在这种情况下乙就会很快知道自己戴的不可能是黑帽子，否则，学生丙将不假思索地立刻猜出自己戴的是白帽子。现在乙和丙都在犹豫，不能马上猜出，说明他们看到甲戴的不是黑帽子，从而甲就能猜出自己戴的必定是白帽子。同样，乙和丙也能猜出自己戴的是白帽子。非常神奇吧？看来聪明的学生能得出一般人认为不可能的结论。

上面的问题只是小学生奥数水平的问题，下面这个“海盗分金问题”稍微复杂些。这个问题首先出现在1999年《科学美国人》杂志上。传说有5个聪明的海盗，一同抢得了100个金币，要进行分赃。这些海盗有严格的等级，按等级高低分别称他们为老大、老二、老三、老四和老五，他们的分配规则还算民主：先由等级最高的海盗提出一个分配方案，然后全体海盗投票决定是否接受方案，如果半数或半数以上的海盗同意，那么就按这个方案分配，否则就将提出方案的海盗扔到海里，由下一个等级最高的海盗重新提出分配方案，并继续投票，依此类推。海盗们以下面的原则作出自己的决定：首先要保命，这当然是最重要的；其次要保证自己的利益最大化，即得到尽量多的金币；最后，在不损害自己利益的情况下，能够害人绝不会仁慈。这里还要对海盗的特性做一下交代，这是一批非常聪明而理性的海盗，他们一定会作出对自己最有利的决定；海盗们还是极端自私的，互不相信他人，不会结成同盟。那么问题来了，老大现在该作出怎样的分配方案？直觉上，老大为保命，大概不能拿得太多，以保证其他海盗通过他的提议。但意外的是，老大提出的分配方案和我们的直觉大相径庭：他给老三、老五各一个金币，老二、老四一个不给，剩下98个金币都留给了自己。难道他不怕其他几个海盗都投反对票，然后把他扔到海里吗？不会的，老大自信这样的方案可让老三、老五投赞成票，加上自己一票，有超过半数的3票来通过他的方案。

为什么呢？要想作出最优的决策，不妨倒过来想一想最后剩下的海盗会作出怎样的决策。假设只剩下老四、老五两个海盗，老四会怎么分配？很明显，老四自己的一票就能保证他的方案会通过，他可以完全忽略老五的存在，把100个金币全部留给自己，老五一个金币都得不到。现在把老三考虑进来。老三要想自己方案获得通过，自己的一票不够，他还需要拉拢一个海盗。老四是无任如何也不会投赞成票的，将老三扔进海里他可以获得最大收益100个金币，因此，老三拉拢的只能是老五。给老五多少呢？一个金币足够了，一个金币总比一无所获强，老五一定会投赞成票。这样，老三的最佳方案就出来了：就是自己拿99个金币，老四一个不给，老五一个金币，即按海盗等级从高到低排列，他的方案是（99，0，1）。接下来，考虑老二参与，老二也只要拉拢一个海盗就行，同样的考虑可知老二只要给老四一个金币即可，即他的方案是（99，0，1，0）。回到一开始的情形，老大的方案就显而易见了，他需要拉拢2个海盗，这只要给老三、老五各一个金币即可，即老大的最佳方案是（98，0，1，0，1），这就是一开始给出的方案。这样，老大既能保命，又获得了最大的利益，看来做老大还是好啊。只是做老大好是好，风险还是很大的。不但要自己聪明，还要手下也个个聪明，要是有一个傻瓜，比如老三傻傻地认为一个金币太少，那老大的性命就很危险了。

要是让老大直接在所有可能的方案中找出最佳方案这是一件十分困难的事，上面这种从一个最简单情形出发逆向递归寻找最优方案是一个非常有效的方法。事实上，前面的“帽子问题”的解决也可以使用逆向递归。由此，我们不难将上述“帽子问题”和“海盗分金问题”推广到更多帽子、更多海盗的情形，对“帽子问题”可推广到n个学生n-1顶帽子的情形；对“海盗问题”则是：当6个海盗时，老大的最佳分配方案是（98，0，1，0，1，0），7个海盗时是（97，0，1，0，1，0，1），依此类推。不过当超过200个海盗时，这个方案需要修改了，因为老大用于贿赂其他海盗的金币不够了，这时，老大是否只有被扔进海里的命了呢？聪明的读者，你能帮老大找到保命方案吗？

上面的问题是在有限多个方案中选出一个最佳方案，如果有无穷多个可选方案，有没有找到最佳方案的可能呢？我们来看看下面的“约会问题”。有两位聪明的经理人，在一个酒吧偶遇，却一见如故，聊得非常投机，相约第二天再在同一间酒吧见面。可能是有点喝高了，他们只约定在0点到1点之间见面，没有讲定具体时间。更糟糕的是，他们只顾聊天，都忘了问对方的联系方式，并且他们知道，经理人都很高傲，先到的人只会等10分钟，10分钟过后等不到人就会离开。那么，这两位经理人能在第二天见到面吗？

显然，两人第二天有可能见上面（两人到达酒吧的时间间隔不超过10分钟），也有可能见不到（两人到达酒吧的时间间隔超过了10分钟），这是一个概率问题。事实上，这个问题是大学概率论教科书中的一个例题或者习题，要求计算两人能够碰面的概率。通常是这样计算的：将经理人甲到达酒吧的时间记为x，经理人乙到达酒吧的时间为y，均以分钟为单位，则0≤x，y≤60。以x为横坐标、y为纵坐标建立坐标系，则甲乙的到达时间（x，y）就落在如图1所示的［0，60］×［0，60］的正方形中。而甲、乙能够在酒吧见面等价于他们到达的时间间隔不超过10分钟，即满足|x-y|≤10，而满足|xy|≤10的点（x，y）落在正方形中两条直线y＝x-10和y＝x+10之间的阴影部分。如果两人到达的时间是随机的，则他们能够碰面的概率就是阴影部分的面积和整个正方形的面积之比，计算得到这个概率是11／36。也就是说他们只有不到1／3的机会见上面。

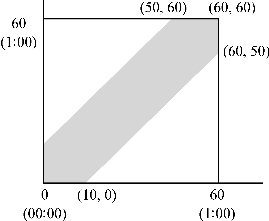
图1(www.daowen.com)

难道说能否再见面只能听天由命？要知道这两个经理人很聪明，他们也相互知道对方很聪明。他们可不会随机地在0点和1点之间的某个时间到酒吧赴约，他们会选择一个他们认为最合适的时间到达酒吧。显然，这个时间不会是0点整，如果经理人甲在0点整到达，那么只有乙在0：00到0：10这10分钟内到达才能碰上，他们能见面的概率只有1／6。往后延一点，比如在0：01到达，则乙在0：00到0：11这11分钟内到达他们都能碰上，见面的机会增加了。甲到达的时间继续向后延，他们见面的机会还会继续增加，直到甲在0：10到达，此时乙只要在0：00到0：20之间到达，他们就能碰上，见面的概率上升到1／3。因此，既然在［0：00，0：10）这个时间区间内到达酒吧，见面的概率不是最大，那么在该时间区间内到达就不是最佳选择，聪明的甲是不会选择在这个时间区间内到达酒吧的，对称地，他也不会选择在时间区间（0：50，1：00］内到达，这样甲的最佳选择应该出现在［0：10，0：50］的某一刻。可是，不管甲在此时间区间内何时到达酒吧，都是当乙在甲到达的前后10分钟内到达才能碰面，见面的概率都是1／3。这似乎在［0：10，0：50］中随机选一个时间到达都一样，无法确定一个最佳时间。

但是，在没有选出一个最佳方案前，甲是不会就此停止思考的。他知道乙和他一样聪明，同样不可能在［0：00，0：10）和（0：50，1：00］内到达酒吧。因此，他们两人都只会在［0：10，0：50］之间到达酒吧，这等于将原来约定的时间区间缩短为一个新的时间区间［0：10，0：50］。当然，时间区间缩短了，他们见面的机会就会增加。更为重要的是，他们可以对新的时间区间做和前面一样的思考，结果是可以将到达的时间区间进一步缩短为［0：20，0：40］。好了，现在可以明白了，这个区间还可以进一步缩短，最佳的时间也就出来了，那就是0：30。毫无疑问，甲和乙都会选择0：30到达酒吧，这对双方来说都是最佳的选择，他们百分之百能再次见面，而且根本就不用等。怎么样，是不是很佩服？读者如果遇到类似的情况，而你的约会对象也比较聪明，不妨试一试这个策略。

上面的例子来自博弈论，是一个关于时间的博弈，而双方选择的时间0：30被称作一个纳什均衡点，这是一个最佳选择，见面机会为100%，等待时间是0。在上面的例子中，博弈的参与者之间无法进行沟通合作，只按自己利益的最大化作出选择，称为非合作博弈，这是著名数学家、经济学家、诺贝尔经济学奖获得者约翰·纳什（John Nash，1928—2015）（就是美国电影《美丽心灵》中的天才约翰·纳什）考虑的问题。而所谓“纳什均衡”是非合作博弈中的这样一个策略组合：博弈的参与者都选定了一个策略，在其他参与者都不改变自己策略的情形下，任何参与者单独改变策略将不会获得更大的利益。因此，纳什均衡是一个稳定的状态，在这个状态下，对每个参与者而言是不得不选择的最优策略。

不过，纳什均衡对博弈的全体参与者来说未必是全局最优的。著名的“囚徒困境”就能说明这个问题。警察抓住了两个窃贼，控告他们犯有抢劫罪。警察将两人分别带到两个隔离的审讯室审讯，并告知他们：如果两人都认罪，将各判5年监禁；如果两人都不认罪，则各判1年监禁；如果一人认罪，另一人不认罪，则认罪者将被释放，不认罪者将被判10年监禁。那么，两个窃贼是选择认罪还是不认罪呢？考虑其中一个窃贼，如果他选择认罪，那么可能的结果是判5年（另一个窃贼也认罪）或者0年（另一个窃贼不认罪）；如果他选择不认罪，那么可能的结果是判10年（另一个窃贼认罪）或者1年（另一个窃贼不认罪）。显然，选择认罪远远好于不认罪，如果两个窃贼都是理性的，他们就都会选择认罪，这样两人各判5年。两人都选择认罪就是一个纳什均衡，但这对两个窃贼来说显然不是最佳的选择，因为他们还有一个更好的选择，就是两人都不认罪，此时他们只各判1年。但是这个最佳方案是不稳定的，他们无法选到这个最好的方案，即使他们在被捕前商量好拒不认罪，在隔离审讯时他们也不敢不认罪：谁能保证对方不会因为那个有可能被释放的诱惑而背叛自己？选择认罪尽管不是最优的，至少还是次优的。

但是，纳什均衡也有可能产生两败俱伤的情况。假设一个小镇上有唯一一家鸭脖店，不妨称其为A记鸭脖店。鸭脖的成本是2元，售价为10元。由于小店的鸭脖做得味道十分鲜美，价格对小镇上的人来说完全能够接受，因此一直生意很好。有一天镇上突然新开了一家鸭脖店，称其为B记鸭脖店，B记的鸭脖做得和A记一样美味，成本售价也完全相同。这样，小镇上买鸭脖的顾客有差不多一半流向了B记。A记显然不能接受这种情况，即出一招：降价到9元销售。这样顾客就全都回流到A记了，A记的生意依然很好。但B记也不傻，立马降价到8元。这样你来我往，激烈的竞争导致两家最终都以成本价2元销售，这就是一个纳什均衡点。每一家都不能再降价，否则将是亏本销售；也不能单独提价，否则意味着没有销量。可见，尽管A记、B记两家店每一步都是为了自己利益最大化，可最终的结果是两家都受损，真是两败俱伤。这种情况在市场恶性竞争中经常出现。

纳什均衡理论是对市场经济中亚当·斯密（Adam Smith，1723—1790）“看不见的手”原理的挑战：按照斯密的理论，在市场经济中，每一个人都从利己的目的出发，而最终全社会能达到利他的效果。但是我们可以从纳什均衡中看到，从利己目的出发，结果损人不利己，既不利己也不利他。可见，市场经济也不是万能的。

复旦大学数学科学学院　邱维元