我们这种物质波的观点与传统的量子力学的观点有何异同之处？首先让我们讨论这两种观点不同的地方，再讨论它们的相同之处。

在本章的开始，我们已经表明，从实验的证据来看，物质波应该是一种拥有具体粒子性质的真实的波。否则难以解释电子的衍射实验及双缝干涉实验。而且，如果我们相信德布罗意的假设的话，电子与光子都应该是真空介质的激发波。具体而言，根据麦克斯韦理论，我们知道真空的物理性质很像一种电介质，里面充满着带正电和带负电的电荷载体。所以不论是辐射波还是物质波，其实都是这些电荷的波动。在我们最近的一篇论文里，对于物质波的性质做过一些详尽的研究。^[5]我们发现，真空介质激发波的传播机制其实与一个弹性固体里的激发波传导的机制有相似的地方。根据这两者的类比，我们得出了一个结论：在量子方程里的波函数与麦克斯韦理论里的“电荷位移” （charge displacement）有着直接的关系。

在传统的量子力学里面，一般采用哥本哈根学派的诠释。在这个传统模式里面，粒子是个点状物体。而量子方程里的波函数只是这个粒子在某一时空存在的概率波；这个波不是真实的波，它只有统计学上的意义。

我们在本章里讨论的物质波观点，虽然与哥本哈根学派的出发点不一样，但其实这个模型也可以得到哥本哈根学派的计算结果。换句话说，如果采用物质波的观点，把微观世界的粒子理解为一种真空的激发波的话，也可以得到波函数与粒子存在的概率关系，而且它的结果与哥本哈根学派所假设的是一致的。

前面已经提到，当一个光子在真空中传播时，整个波包的长度起码是几十微米，相当于几十万个原子的长度。但是当这个光子被原子里的电子吸收时，整个光子的能量都会集中到一个电子身上。所以，当一个光子在传播时，很多个原子都可以同时感受到这个光子的存在，但最终只有一个原子里的电子能够把光子的能量全部吸收，这就表示光子与电子的互动很大程度上是依赖概率的。那么当这个光子在某个时刻与众多原子同时互动时，哪些原子有较大的机会能够吸收到光子的能量呢？这当然就要看这个原子所处的位置是否有利于吸收光子的能量。

打个比方说，每一个有可能吸收光子的原子就等于是一个“天线”。它可以吸收天上的无线电波（相当于光子的波包）。如果这根天线处在波包振幅最大的地方，它感受到的信号最强，因此它能吸收到这个光子的可能性就最大。反过来说，如果一根天线处在一个波包振幅很小的地方，天线所感受到的信号就很弱，它吸收到这个光子的可能性就很小（见图6.11）。

在这个以原子作为天线的类比中，我们可以粗略地估计在不同位置的原子能够吸收光子的概率。一根天线接收到的电信号的幅度应该与该天线位置辐射波的强度成正比，天线所产生的电信号的强度可以用一个电位差V(x)来量度，辐射波的强度可以以波函数ψ(x)来量度。因此，这个电位差V(x)与ψ(x)波函数的绝对值成正比：

假如我们把天线吸收的能量称为E(x)，由于E=V2/R，所以E(x)与V(x)的平方成正比。根据上式，我们就可以得到：

(www.daowen.com)

图6.11　解释原子位置与吸收光子波包关系的示意图

要测量光子的位置就需要使用一个光子的接收器。这就好像要使用一个天线来接收无线电波信号，而这个电波信号其实是一个波包。处于波包振幅最大的地方的天线能吸收到这个光子的可能性就最大，处在一个波包振幅很小的地方的天线吸收到这个光子的可能性就很小。

也就是说，一个光子可以同时与很多个原子互动。但只有一个原子可以吸收这个光子（注：这是由于“整或零原理”）。那么哪一个原子可以这么幸运呢？我们认为，那些有可能吸收到最多光子能量的原子，能最终掳获光子的概率就最高。换句话说，一个原子吸收这个光子的概率是与上述的E(x)成正比的。根据上式得到：

原子在x位置吸收光子的概率～|ψ(x)|2

上述的讨论是以光子为例子。不过，根据我们的物质波模型，电子与光子都是真空的激发波。因此一个电子的吸收概率也有相似的关系。如光子一样，一个自由的电子的波包也可以分布很广。如果一个实验者要侦测这个电子的位置，他必须使用一些实验手段来让这个电子被某个原子吸收。当这个电子被吸收时，这个自由电子的波包就会在瞬间崩塌，把全部的能量和电荷转移到一个原子里面去。所以在做实验以前，这个自由电子只是一个波包，它的“粒子”位置是不能确定的。只有在进行了检测实验以后，这个电子的波包才会崩塌到一个原子之中，这时候，人们才能确定这个电子“粒子”的位置。由于这个波包在未崩塌时，可以覆盖多个原子，许多原子都有机会吸收这个电子。那么在哪些位置的原子吸收电子的机会比较高呢？从上面分析光子的吸收过程中，我们就可以知道，当一个原子感受到电子波包的振幅较大时，它与这个电子的互动也就较强，因此吸收这个电子的概率也就较大。在这个过程里，一个在x位置的原子能吸收该电子的概率也会与上式一样，与电子在x位置的波函数的平方成正比（见图6.12）。

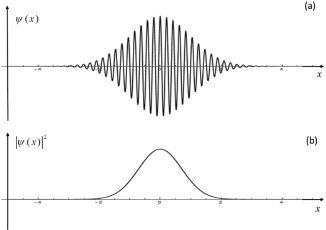
图6.12　波函数与侦测到粒子概率的关系

一个自由的电子的波包分布很广。只有当这个电子被原子吸收时，它的波包才会在瞬间崩塌，把全部的能量和电荷转移到一个原子里面去。所以在做实验以前，这个电子的位置是不能确定的。只有在这个电子的波包崩塌以后，人们才能确定这个“电子”的位置。从上面分析光子的吸收过程中，我们可以知道，当一个原子感受到电子波包的振幅较大时，它与这个电子的互动也就较强，因此吸收这个电子的概率也就较大。一个在x位置的原子能吸收该电子的概率与电子在x位置的波函数的平方成正比。（a）ψ(x)是电子的波函数；(b)|ψ(x)|2是电子的波函数的平方，它与电子被检测到的概率成正比。

所以，即使采用了这个物质波的观点来解释量子方程里的波函数，也可以得出哥本哈根诠释预言的结果。