根据上述的思路，我们就有办法找出量子力学里面常用的波动方程（包括狄拉克方程与薛定谔方程）的物理基础。我们发现，辐射波和物质波方程都可以从麦克斯韦理论中导出，而从这个物质波方程，最终就可以导出薛定谔方程^[3]。这个推导的过程可以用图6.10来说明。

首先，从麦克斯韦方程我们可以得到真空的激发波方程。其次，这个激发波方程可以有两类的解：第一类是平面波（plane wave），它代表着电磁的辐射波；第二类是类似于旋涡的波（vortex wave），它代表着描述粒子运动的物质波。对于辐射波，真空的激发波方程可以直接变成光的波动方程（见图6.10）。对于物质波，真空的激发波方程可以导出克莱因-戈登方程。再次，当这个粒子是一个费米子（如电子）的时候，克莱因-戈登方程可以导出狄拉克方程。最后，当电子的运动在一种低能量的状态下，狄拉克方程可以转变为薛定谔方程。

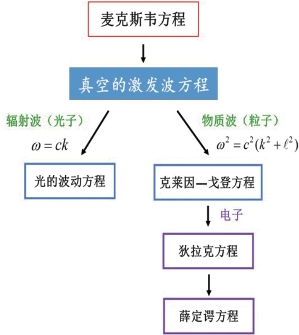
图6.10　电子的量子波动方程的物理基础

根据我们建议的物质波模型，粒子只是真空的激发波。而真空的物理性质可以从麦克斯韦理论里面知道。因此，不只光子的波动方程可以从麦克斯韦理论里导出来，电子的量子波动方程也可以从麦克斯韦的理论里导出来。换句话说，辐射波和物质波都是同源的。不过，两者的色散关系并不一样。（详细的推导过程可以参考D.C.Chang,(2021) Review on the physical basis of wave-particle duality: Conceptual connection between quantum mechanics and the Maxwell theory.Modern Physics Letters B,Volume 35,Number 13;2130004）

在上述这项推导过程中，我们发现辐射波和物质波虽然都是真空的激发波，但这两者有着不同的“色散关系”（dispersion relation）（色散关系是指波的频率与其波长的关系）。这一点非常重要。因为我们知道，一个波包的运动速度是由其色散关系来直接决定的。当这个色散关系不一样的时候，这个波包的运动速度也就不一样了（见附录6.1）。

附录6.1：波包在介质中的运动速度

当一个波包在介质中传播时，波包的运动速度并非由波的“相速度”（phase velocity）决定，而是由波的“群速度”（group velocity）决定。后者又取决于波的色散关系。更具体地说，波包的群速度就等于波数对频率的一次微分：。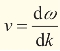

我们在上一段已经指出，真空的激发波可以用两种不同的模式传播。第一种是辐射波，第二种是物质波。辐射波的色散关系是：

(www.daowen.com)

由于

所以，这种色散关系意味着光的传播速度是恒定不变的（也就是光速c）。

对于物质波，它的色散关系是：

因此，

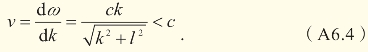
其中：l=2π/λCompton。l与康普顿波长成反比，因而与粒子的质量成正比。式（A6.4）意味着物质波的波包（代表着一个粒子）的运动速度不是恒定的。一个粒子（波包）的速度最多只能达到光速c。而且，根据德布罗意关系，一个粒子的动量与它的波数k成正比。因此，物质波的色散关系就表示：一个粒子的动量越大，它的速度也会越快。