上述的粒子观点可以说是传统量子物理学的主流观点。不过，如我们在上一章里面所述，粒子观点无法解开量子世界里面的一些困惑。因此，在下一个发展阶段里，人们应该尝试用另外的观点来解释量子理论。而这个观点就是把物质波当成一种真实的、具有粒子性质的激发波来看待。

我们认为，粒子其实只是真空介质的激发波。打个比方，真空就像一个池塘。当你向平静的池塘里扔一块石头，你会激起一个波浪。这个波浪实际上就是水的激发波。当你向真空里施加一点能量，就会出现一个粒子，这个粒子就是真空的激发波。

如果粒子真的只是真空介质的激发波，我们很容易理解为何能量对真空的激发能够产生新的粒子。对于波浪而言，它只是其介质的一种运动形式（见图6.6）。如果一个粒子只是真空介质的一个激发波，它自然可以“无中生有”。

我们知道任何一种波动传播都需要介质。例如，当你和你的朋友聊天，声音（声波）通过空气传播，你才能听到朋友的声音。如果空气被抽空，你就无法听到朋友的声音了。你可能会问：如果粒子真的是就像池塘里的水波，那么这里的“水”是什么呢？什么是粒子的介质呢？我们认为这就是真空本身，也可以称之为“真空介质”。对于真空的物理性质的详细讨论，我们会在稍后进行。

对于这个把粒子视为真空介质的激发波的想法，你可能会问，这个想法有何依据？这就要回到我们在第五章里介绍的波粒二象性。对于光子而言，我们老早就知道它是一种电磁波。这是一种真实的、具有粒子性质的波。在过去几个世纪对光的波动性的研究中，并不都是这样的观点，一些科学家一直认为光波是真空的激发态。通过麦克斯韦的理论，我们也的确知道光是一种电磁波，也同时是真空的激发波。而且，满足普朗克关系和德布罗意关系，

(www.daowen.com)

图6.6　能量以波的形式在介质中传递

正如波浪是水的激发波，我们相信粒子也是真空介质里的激发波。唯一的区别是，后者是一种量子化的波包，波的能量和动量都有一个最小的值。这个代表粒子的波包在产生、传递和湮灭的过程中，都必须符合一项“整或零原理” （Principle of allor-none）。

其中：ω是光的振荡频率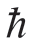，是普朗克常数除以2π，p是动量，k是波数。我们知道光同时具有粒子性质和波动性质，而且这两种性质是互相对应的。根据德布罗意的理论，许多具有静止质量的粒子（包括电子等）也具有波粒二象性，与光子相似。因此，我们把粒子当作真空介质的激发波只是根据德布罗意理论的进一步的推广。

我们一旦把粒子作为一种激发波，不但可以很轻易地解释为何在对撞实验里会出现的新的粒子，还可以很容易地解释衍射实验以及双缝干涉实验里观察到的波粒二象性。下面是较为详细的解释。