有了薛定谔的电子波方程，人们就可以计算电子在原子里的分布。这时候人们发现把原子的内部结构当作一个小型太阳系不是完全准确的。电子在原子里的运动不像行星的轨道，而更像某种振荡的波。也就是说，电子在某个时间内在原子里面的位置并非是一个特定的点，而是分布在某一个特定的空间之内，这个电子分布的空间就被人们称为“电子云”。

为了说明这个薛定谔方程对于人们了解原子结构的贡献，我们可以以氢原子为例。氢原子是最简单的原子，因为它只有一个电子。利用薛定谔的波方程，人们可以很容易地解出氢原子中的电子的波函数。人们发现这个波函数可以有多个不同的解，每一个解包含有4个量子参数：

（1）主量子数n（相当于玻尔模型里的n）;

（2）角动量量子数l（azimuthal quantum number）;

（3）磁量子数m（magnetic quantum number）;

（4）自旋s（spin）。

因此，我们可以把这个波函数写为ψ（n，l，m，s）。要使得这些波函数满足薛定谔的波方程，这些参数要符合以下的要求：首先，n必须是正整数；l也是整数，它的取值可以从0到n-1；m是l的投影，m可以是正或者负的整数，但它的绝对值不能大于l。电子的自旋s只有两个值，就是-1/2 或+1/2（见表3.1）。

表3.1　量子参数的取值规律

对于这些电子波函数ψ的不同的解，物理学家认为这代表着电子在氢原子里的不同“轨道”。打个比方，这就像在一个行星系统里，可以有多个行星轨道。当原子里的电子处于不同的能级时，它就会占据不同的轨道；也就是说，该电子形成了不同形状的电子云。(www.daowen.com)

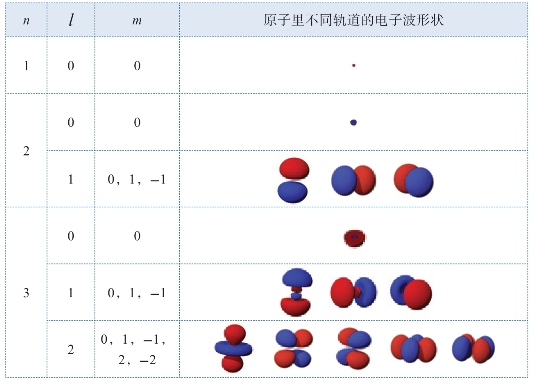
下面让我们看看这些不同的电子波函数的具体形状（见表3.2）。我们在前面说过，这些电子波函数包括四个量子参数，就是n，l，m，s。前三个量子参数决定了这些电子波函数的分布形状。最后一个参数仅代表电子的自旋是正或负。表3.2给我们列出了n=1，2，3的电子波函数形状。从表里可以看出，当l=0的时候，电子波函数的分布基本上很像一个球体。但是当l >0的时候，电子波的形状就会变得复杂得多。

表3.2　不同电子轨道的电子波形状

使用了薛定谔方程，人们不但能够计算氢原子里面的电子波函数的分布，人们也可以计算含有多个电子的原子的波函数。人们发现，不论原子里面的电子的数目是多少，基本上每个电子的波函数还是根据上面提到的4个量子参数来决定的。而且，这些参数的规律也和表3.2所示的相同。

综上所述，具有不同量子参数的波函数，代表着原子里不同能级的电子轨道。一般来说，当n的数值越大，代表着能级越高的电子轨道。电子可以在两个不同能级的轨道之间跳跃。当它从高的能级跳到低的能级，电子就会释放能量。这种被释放的能量以电磁辐射（光子）的形式发出。相反，如果一个电子想要从一个低能级的轨道跳到一个高能级的轨道，它就需要吸收外界的能量（如某种特定波长的光）。

图3.9　泡利

Wolfgang Pauli,（1900—1958）是奥地利理论物理学家。他的博士生导师是著名的德国物理学家索末菲。他在量子力学里做了大量的工作，最知名的贡献就是发现了“泡利不相容原理”，并因此获得了1945年的诺贝尔物理学奖。