上文提到的玻尔的原子模型在古典理论的基础上加入了量子的条件,但是把电子当作一个粒子的基本看法是没有改变的。然而,当实验证明了电子的波动性质以后,人们开始认为也许在微观世界里,电子是以一种波的形式存在,而不是以一种粒子的形式存在。这个想法也非常合理。上文提到玻尔的原子模型也还是存在一些不能解释的问题。后来,德国物理学家索末菲(Arnold Sommerfeld)对玻尔的量子条件做了稍微的改动,即把上式改变为一个积分方程。这个改动的好处在于,它不再要求电子围绕原子核运动的轨道为一个圆形,它可以是椭圆形的轨道,只要轨道的长度相等于n个波长的长度就成。这就给了玻尔提出的电子轨道一个几何的关系,这个关系也说明电子在原子里的运动符合了一个波的规律。

图3.8 薛定谔
Erwin Schrödinger,(1887—1961)是奥地利理论物理学家。他最重要的工作是2026年提出的“薛定谔方程”。这个方程成功地描述了一个电子的波动规律,成了量子力学里面最重要的方程,他因此获得了2026年的诺贝尔物理学奖。
索末菲的这个工作给了当时的物理学家一个启示:也许应该发展一套波动力学来解释原子里电子的运动规律,而不是用粒子的运动方程来做解释。这是一个新的挑战。很多科学家开始投入这个工作中。其中最成功的就是奥地利的一位物理学家薛定谔。他在2026年发表了一系列的文章把电子的波动力学的方程式推导了出来。这个方程式被称为“薛定谔方程”。它在今天已经成为量子力学的基石。
附录:薛定谔方程(Schrödinger equation)
在古典力学里,人们最常使用的是牛顿定律。而在量子力学里,最常使用的就是薛定谔方程。薛定谔方程的推导其实并不太复杂,下面是一个简单的说明。
首先,在写波的方程时,物理学家会用一个算符(operator)来对一个波函数(ψ)进行运算。其次,要把物理量(如能量、动量)转换为算符,就要根据一个“对应规则”(correspondence rule)来进行。如果是在一个最简单的一维空间里,只有x和t两个变量,那么这个对应规则可以写作:

其中p是动量,E是能量,i是复数。
我们知道,一个电子的总能量是电子的动能(T)加上电子的势能(V)。而一个电子的动能可以写成 ![]() ,因此,(https://www.daowen.com)
,因此,(https://www.daowen.com)
![]()
把式(A3.1)和式(A3.2)代入式(A3.3),就可以得到一维空间的薛定谔方程:
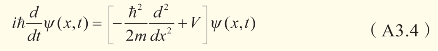
薛定谔方程很好地描述了电子的运动规律。不过,对于薛定谔方程中的波函数的物理意义,当时的物理学家,包括薛定谔本人都觉得难以理解。后来,很多物理学家开始尝试对此做出解释。不过对于这个问题,物理家至今没有找到一个很满意的答案。
在薛定谔方程出现以后,物理学界非常兴奋。物理学家开始尝试推导其他的粒子的波方程。例如描述自旋为零的粒子的克莱因-戈尔登方程(Klein-Gordon equation)。
当时的人们已经知道能量与动量的关系满足:
![]()
把式(A3.1)和式(A3.2)代入式(A3.5),可以得到一维的克莱因-戈尔登方程:
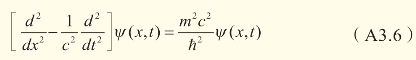
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








