在科学的发展过程中,会不断出现新的模型。这些新的模型是否会被后来的人采纳,主要看它是否能比过去的模型更容易地解释实验观察结果,或者是否能解释更多的事实。我们在上面介绍的物质波量子模型,它显然比传统的粒子量子模型能解释更多的在微观世界里观察到的物理现象。不但如此,它还为量子理论提供了一些更清晰的物理基础。从上面的讨论可知,这个物质波模型可以解决过去许多对于量子理论的困惑,包括:
(1)粒子为何能在真空中产生和湮灭?
(2)为何粒子会有波粒二象性?
(3)物质波的物理性质是什么?
(4)对于爱因斯坦与玻尔关于量子波函数不同解释的争议,如何能提供一个比较合理的解答?
除此之外,这个物质波模型还可以解决量子力学里面一个很重要的难题:如何去解释海森堡的测不准原理的物理基础。
人们如果把粒子视为一个微小的质点,是没有办法解释海森堡“测不准原理”的物理依据的。这个原理只能当作是一种理论上的假设。但如果我们采用物质波的观点来看待自然的微观世界,那么这个测不准原理就可以很容易解释。[6]
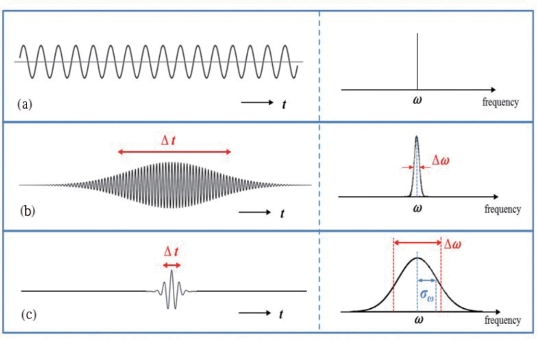
根据我们的物质波模型,粒子只是一个量子化的真空介质的激发波。由于粒子是以一个波包的形式运动,它的频率(ω)与波长(λ)并非单一的,而是有一个狭窄的范围(例如波包的频率主要分布在的范围内ω±Δω)。对于一个波包来说,它在空间和时间维度上也都会有一定的宽度,Δx和Δt。我们从数学上的傅立叶变换(Fourier transform)的分析中得知,Δω与Δt是互相对立的,当一个波包的Δω越小,这个波包的Δt就会越大;反之亦然(见图6.13)。当一个波包是接近于一个连续波的时候,它在时间轴上是非常宽的,也就是说它的Δt非常大。但同时,这个波包的频率就会非常接近一个单一的频率,也就是说它的Δω会变得接近0[见图6.13(a)]。反过来说,如果这个波包在时间轴上是非常窄的(Δt→0),那么这个波包在频率上的分布就会非常宽(Δω会变得非常大)[见图6.13(c)]。
对于一般的波包,Δω与Δt都不会趋近0[见图6.13(b)]。这时候,根据数学上对于傅立叶变换的要求,波包的频率宽度和时间宽度必须满足下列的数学关系:
![]()
 (https://www.daowen.com)
(https://www.daowen.com)
图6.13 波包在时间上的宽度与其在频率上的宽度的关系
左侧的图代表时间的领域,右侧的图代表频率的领域。(a)当一个波包是连续波时,它在时间领域中分布很广;它的频率ω却是一个单一的常数。(b)当一个波包在时间上有一定的宽度时,它的频率分布也有一定的宽度。(c)当一个波包在时间上是非常窄的时候,它的频率的分布就会变得较为宽阔。
利用了普朗克关系![]() ,从上式就可以得到:
,从上式就可以得到:
![]()
以上的关系式描述了一个自由粒子的波包在时间与能量上的不确定性,这就是海森堡“测不准原理”。应用了数学上的傅立叶变换的分析,我们还可以得到一个粒子波包在位置和动量上的不确定性。假定粒子是真空介质里的一个波包,它的位置和波数的分布宽度分别为Δx和Δk,根据数学上对于傅立叶变换的要求:
![]()
利用德布罗意关系![]() ,从上式就可以得到:
,从上式就可以得到:
![]()
以上的关系式描述了一个粒子的波包在位置和波数上的不确定性。所以,为何自然中的粒子会符合海森堡的“测不准原理”,这完全是因为一个粒子在本质上是一个波包。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






