例13－6　（旅行售货员问题）　现有一位旅行售货员欲到城市v1，v2，…，vn进行商品销售.已知从城市vi到城市vj旅途所需时间为wij＝W（vi，vj）（i≠j，i，j＝1，…，n）（如表13－26所示）.今他从n个城市中的某一个城市出发，试问他应如何计划他的旅行路线，使他对每个城市恰好进行一次访问后又返回出发城市，而旅途所花费的时间最少？

表13－26

解　我们给出启发性算法.

例13－7　某仓库v1的发货员接到6家商店v2，v3，v4，v5，v6，v7的零件订货单.他现从v1出发，到各家商店送货，再回到v1.从vi至vj的送货时间W（vi，vj）（单位：分钟）由表13－27给出.试求一条较好的路线，使他在途中花费的时间最少.

解　由表13－27知：min｛W（vi，vj）｜i，j＝1，…，7｝＝W（v6，v7）＝10＝W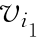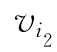（，），划去第6行、第7列及元素W（v7，v6）.

在第7行未划去的元素中选取最小元素W（v7，v1）＝35，令W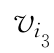（，）＝W（v7，v1），划去第7行、第1列及元素W（v1，v7），在第1行未划去的元素中选W（v1，v3），继续迭代.我们将运算过程列成表13－28.

表13－27

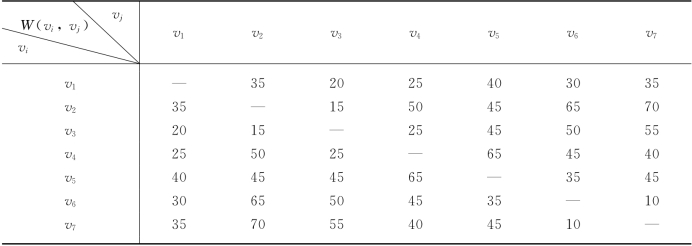
表13－28

我们得一条回路v6v7v1v3v2v5v4v6，它的等价的送货路线为v1v3v2v5v4v6v7v1.送货路上花费的总时间为235分钟.

对于用最近邻点启发性算法求得的旅行售货员问题的较优回路，可以用下列调整算法作进一步的改进.但应注意，这种调整算法仅适用于对任vi≠vj，有W（vi，vj）＝W（vj，vi）的一类旅行售货员问题.

如图13－12所示的旅行售货员回路P：

图13－12

比回路P好.

于是，我们有如下调整算法：

①取一条初始回路P（13－8）（可用最近邻点法得到）.

②是否存在j，k（1＜j＋1＜k＜n），有式（13－9）成立？

若是，则取回路P′（13－10），令P＝P′，转步骤②；

若否，则算法终止.(www.daowen.com)

我们对例13－7求得的回路P＝v1v3v2v5v4v6v7v1进行调整.由图13－13可知

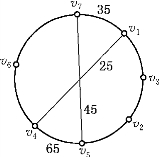
图13－13

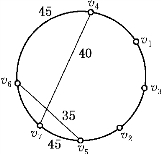
图13－14

故图13－13所给回路P可以调整为图13－14所示的回路P′＝v1v3v2v5v7v6v4v1.由图13－14可知

故对P′又可以调整，得回路P＊＝v1v3v2v5v6v7v4v1，它所花费的总时间为

我们都知道，当不同型号的产品在某部机床上进行机械加工时，若机床对某种型号产品加工完毕而要对另一种型号的产品进行加工时，通常，工艺装备需要更换，换言之，需要花费一定的工艺装备更换时间.产品的加工顺序不同，所花费的工艺装备更换时间的总和也就不同.因此，这个排序问题就是要找一个不同类型产品的最优加工排序，使工艺装备更换时间的总和最少.这个问题好似机床（旅行售货员）要对每个型号产品（城市）访问一次，但不要求再回到起始点（被首先加工的产品）.

例13－8　有4种产品在某种设备上加工.产品vi加工完毕后若接下来准备加工产品vj，则更换工艺装备需更换时间wij分钟，由表13－29给出.寻求一种加工排序，使总的更换时间较短.

解　对本问题我们采用另一种启发性算法.

第一步，选表13－29中最小元素（同时有几个最小元素，可随便选取其中一个）.如现在选w12＝10，将v1行及v2列划去，同时还划去元素w21，见表13－30.

第二步，继续选取表13－30中未划去的元素中的最小元素，可知为w31＝10.这时，我们要检查一下，将边（v3，v1）加到集合｛（v1，v2）｝中会不会产生回路？这里得路径v3v1v2，没有产生回路，故划去v3行及v1列（元素w13已被划去），得表13－31.

表13－29

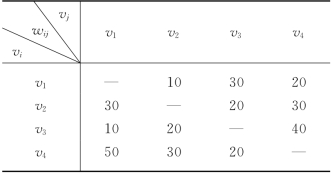
表13－30

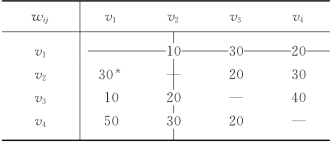
表13－31

第三步，选表13－31中留下的元素中的最小元素.若选w23，那么，将边（v2，v3）加入到集合｛（v1，v2），（v3，v1）｝中可得回路v2v3v1v2，故不能选w23.我们在其他元素中选最小元素，例如选w43＝20.可知将边（v4，v3）加入集合｛（v1，v2），（v3，v1）｝中不会产生回路.

于是，我们得加工排序为v4，v3，v1，v2，所花费的工艺装备替换时间总和为