3台机器B1、B2和B3加工n个工件A1，…，An.每个工件先经机器B1加工，然后由机器B2加工，再由机器B3加工，且3台机器加工此n个工件的顺序必须一致.设机器Bi加工工件Aj的时间为tij（i＝1，2，3；j＝1，2，…，n）.问这n个工件应如何排序，使总完工时间T最小？

对这类排序问题我们采用分支定界法来求解.

若ω＝（ω1，ω2，…，ωn）为1，2，…，n的一个排列，则3台机器按照排序ω加工n个工件时的总完工时间记为T（ω）.对排序ω，我们可构造一个赋权有向图D（ω）如图13－4所示.

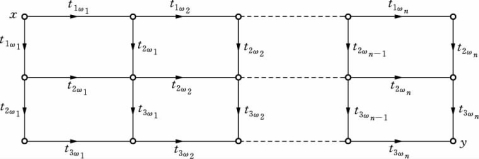
图13－4

定理13－5　D（ω）中顶点x至顶点y的最长路径长度为T（ω）.

下面我们通过一个实例来说明求解该排序问题的分支定界法的基本步骤.

例13－5　一个“3台机器加工5个零件的排序问题”的有关信息由表13－12给出.求最优排序，使总完工时间最小.

表13－12

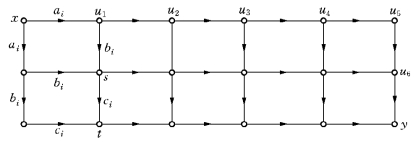
图13－5

表13－13

在表13－13的表（＊）中指出，工件A1固定为第一位加工，而A5，A4，A3，A2这个排序的给出，是用前面所给的算法对两台机器B2，B3加工4个工件Aj（j＝2，3，4，5）这个排序问题求最优排序而得到的，其完工时间即相应网络中源x至汇y的最长路径长度，在表（＊）中我们是用折线标明（以下类同）.

表13－14

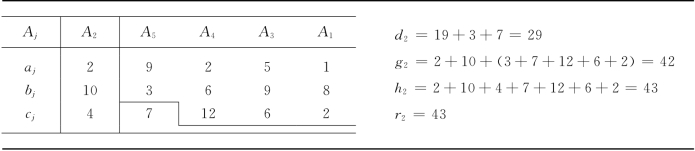
表13－15

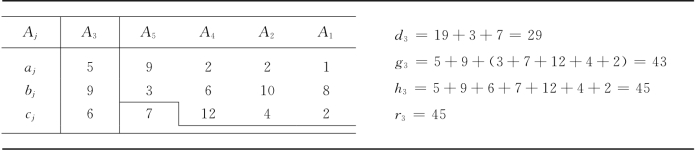
表13－16

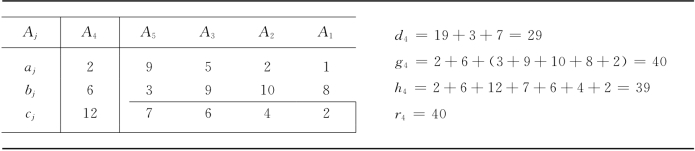
我们得枚举树如图13－6所示.由于问题（K4）的下界最小，故先对（K4）进行分支.

表13－17

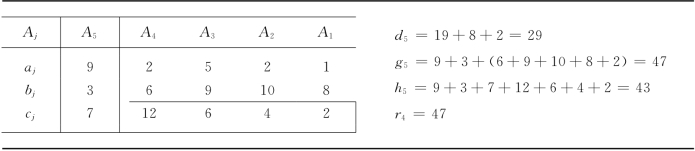
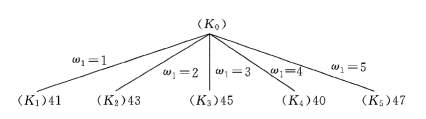
图13－6

第二步，将K4划分为4个子集：

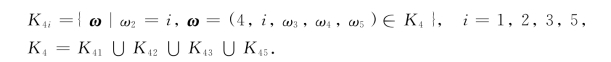
记问题min｛T（ω）｜ω∈K4i｝为（K4i）.

若问题（K4i）的最优排序为ω4i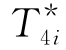，为相应网络图D（ω4i）（见图13－7）中源x至汇y的最长路径的长度，我们对问题（K4i）的最优值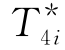的下界进行估计.

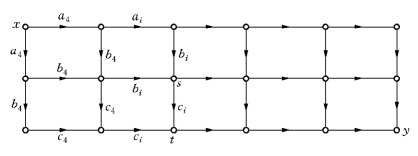
图13－7

类似于第一步中对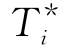的下界估计的讨论，我们有如下结论：

(www.daowen.com)

具体的计算过程由表13－18至表13－21给出.同前面一样，图13－7中x至s或t的最长路径在表中用折线表示.

表13－18

表13－19

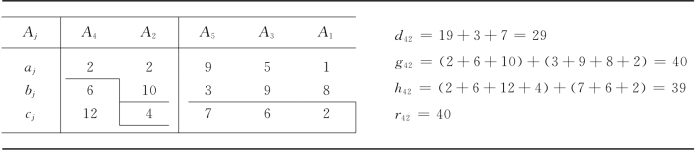
表13－20

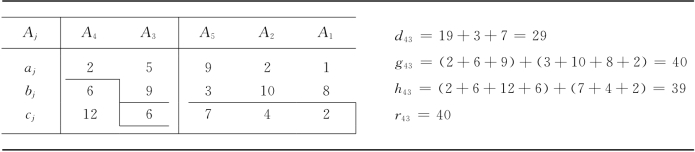
表13－21

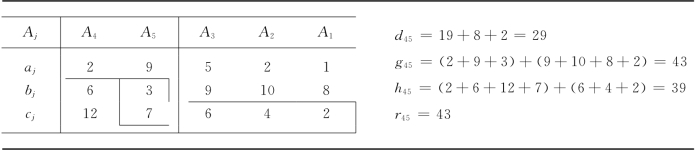
由于问题（K42）的下界是现有活问题（K1），（K2），（K3），（K5），（K41），（K42），（K43），（K45）的下界中最小者，所以我们对问题（K42）先进行划分.

第三步，将K42划分成3个子集：

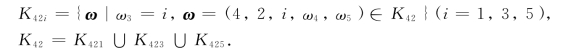
记问题min｛T（ω）｜ω∈K42i｝为（K42i）.

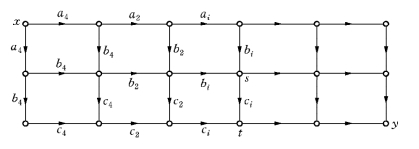
图13－8

具体的计算过程由表13－22至表13－24给出.

表13－22

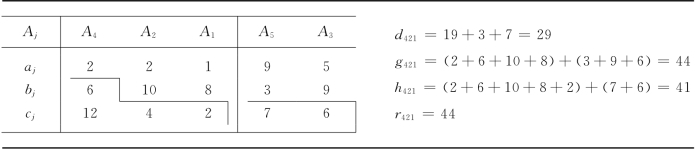
表13－23

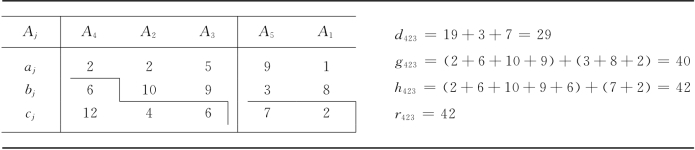
表13－24

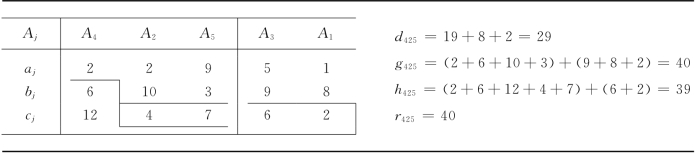
现在诸活问题中下界最小者为问题（K425），我们对（K425）进行划分.

第四步，将K425划分为2个子集

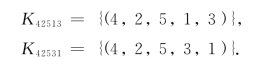
我们得到（K0）的两个可行解（4，2，5，1，3）和（4，2，5，3，1），这两个排序相应的网络如图13－9和图13－10所示，可知它们的总完工时间＝44和＝40.

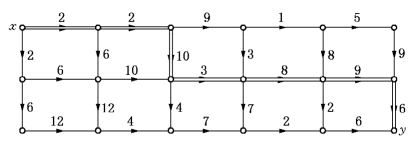
图13－9

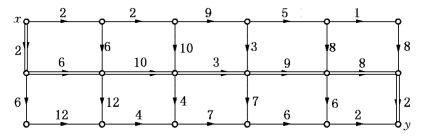
图13－10

我们取定界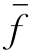＝40，ω＊＝（4，2，5，3，1）.枚举树（见图13－11）上所有活问题的下界都不小于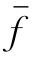，都可剪支，枚举树生长完毕.最优排序ω＊＝（4，2，5，3，1），总完工时间T＊（ω＊）＝40，见表13－25.

表13－25

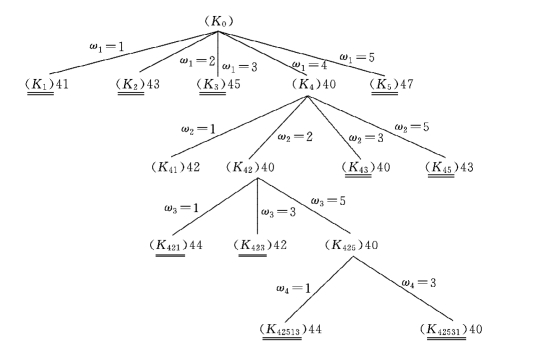
图13－11