例13－4　现有n个零件A1，A2，…，An，这些工件都必须先经机器B1加工，再在机器B2上加工，且规定机器B1，B2加工工件的排序必须一致.已知机器Bi加工工件Aj的时间为tij（i＝1，2；j＝1，…，n）.问这n个工件应如何排序（假设机器B1开始加工第一个零件的时刻为零），使机器B2加工完最后一个工件的总完工时间T最早？

解　设ω＝（ω1，…，ωn）为一种排序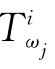，表示机器Bi完成j个工件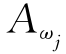，…，加工时的完工时间，显然有

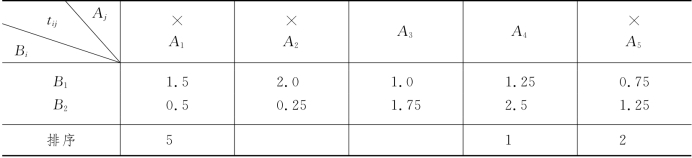
表13－8

表13－8中列出的诸加工时间tij的最小值为t22＝0.25，它为机器B2加工工件A2的加工时间，所以我们将工件A2放在加工排序的末尾，如表13－9所示，并从表13－9中删去工件A2所在列.

表13－9

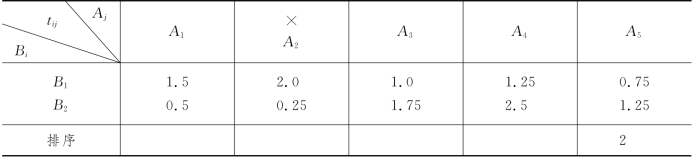
接着我们求表13－9剩余tij中最小值，得t21＝0.5，它是机器B2对工件A1的加工时间，因此将工件A1填入表13－9中排序一行最后一个空格，并从表13－9中删去工件A1所在列，如表13－10所示.

表13－10

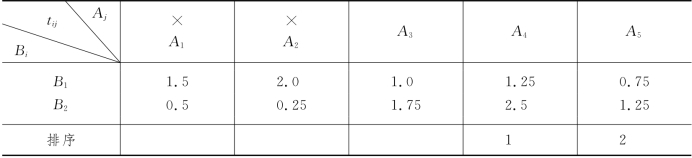
在表13－10剩余tij中求最小值，得t15＝0.75，它是机器B1对工件A5的加工时间，因此将工件A5填入表13－10中排序一行第一个空格，删去工件A5所在列，如表13－11所示.

表13－11

(www.daowen.com)

表13－11剩余tij中最小值为t13＝1，故将工件A3填在排序行工件A5后面.此时剩下唯一的工件是A4，故A4置于排序的第三位.所以本问题的最优排序为（5，3，4，1，2）.它的加工进度表如图13－1所示，它的总加工时间为7个小时，如果机器B1在8：00开始加工工件A5，则15：00所有工件加工完毕.

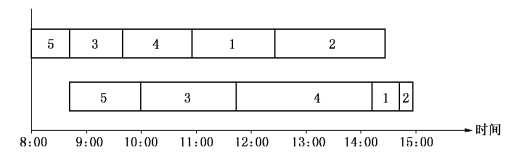
图13－1

对于排序ω＝（ω1，ω2，…，ωn），我们可构造一个赋权有向图D（ω）如图13－2所示.

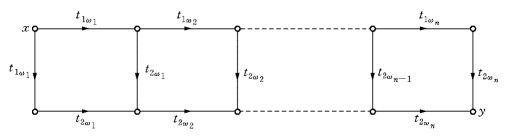
图13－2

定理13－4图D（ω）中顶点x至顶点y的最长路径的长度即为按排序ω加工工件的总完工时间T.

例如，表13－8所给问题的最优排序ω＝（5，3，4，1，2）所对应的D（ω）如图13－3所示，其最长路径P＝xv1v2v4v6v8y，长度为7.

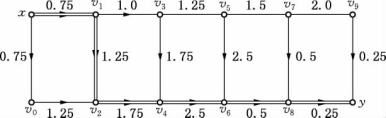
图13－3

我们将两台机器加工n个工件的排序问题的算法归纳如下.