例13－1　设一个机修车间（可以把它看作一台机器）有n台不同的机床（可以看作为工件）要进行大修.它们的维修时间已知为t1，t2，…，tn.而机床Ai在车间逗留的过程中，每单位时间的损失费为wi（i＝1，…，n）.试求一种排序，使得n台机床在修理完毕时，总的损失费为最小.

我们知道，n台机床有n！种不同的排序.此数可能会相当大.例如n＝15，则n！≈1.3×1012.因此，要将所有可能的排序列出来并对它们逐个地加以分析，是不切合实际的.

令集合

由此可知，满足下列条件的排序（r1，r2，…，rn）即为本问题的最优排序：

表13－1

现在若n＝4，有关数据由表13－1给出.可知，最优解排序为（2，4，1，3）.

此时，T2＝6，w2T2＝6；T4＝6＋9＝15，w4T4＝18；T1＝6＋9＋4＝19，w1T1＝9.5；T3＝6＋9＋4＋7＝26，w3T3＝20.8.

总损失费

例13－2　设有n个工件A1，A2，…，An需要在一台机器上加工，加工时间分别为t1，t2，…，tn.试求一种加工排序，使得工件在这台机器上平均停留的时间为最短.

显然，本问题即为例13－1中wi＝1／n的特例.故由式（13－2）知，满足下列条件的排序（r1，r2，…，rn）即为最优排序：

设n＝7，工件Ai的加工时间ti由表13－2给出.

表13－2

表13－3

因为t2＜t3＜t7＜t6＜t4＜t1＜t5，故最优排序为（2，3，7，6，4，1，5）.此时，Ti经计算由表13－3给出.故平均停留时间为(www.daowen.com)

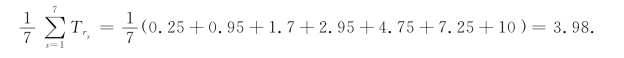
例13－3　设有n个工件A1，A2，…，An要在一台机器上加工，加工时间分别为t1，t2，…，tn，要求的交货日期分别为D1，D2，…，Dn，试求一种加工排序，使得误期交货的工件最少.

我们给出定理13－2.

若否，则算法终止.集合R中元素个数为误期工件个数（R为有序集合）.

例如n＝8，ti及Di由表13－4给出.

表13－4

按算法步骤①，取R＝∅，初始排序（5，4，8，3，2，6，7，1），得表13－5.

表13－5

在表13－5中，可知

k＝2，＝max｛｜i＝1，2，3｝＝max｛4，1，6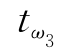｝＝＝6＝t8，故m＝3，ωm＝8，取R＝｛8｝，得表13－6.

表13－6

在表13－6中，可知

k＝5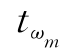，＝max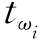｛｜i＝1，…，6｝＝max｛4，1，3，6，8，7｝＝＝8＝t6，故m＝5，ωm＝6，取R′＝R∪｛6｝＝｛8，6｝，得表13－7.

表13－7

由表13－7可知，按排序（5，4，3，2，7，1，8，6）加工零件的误期工件最少，有2个工件误期.