如何通过与决策者对话建立相应的效用函数呢？对于一个决策问题，如果最小收益值为a，最大收益值为b，我们以收益x为自变量，［a，b］上的效用函数设为u（x），并有u（a）＝0，u（b）＝1.对于x∈［a，b］，u（x）称为x的效用值，u（x）∈［0，1］.

例如，在上面一个问题中，最大收益为500万元，最小收益为（－300）万元，我们就规定u（x）定义在［－300，500］上，而且u（－300）＝0，u（500）＝1.下面我们先来看，对于x＝50∈［－300，500］，u（50）如何确定？我们采用对比提问法.

如前面所讲，决策者宁愿采用稳得50万元的策略，而不愿采用收益期望值为240万元的策略.它说明在决策者心目中，稳得50万元的策略S2的效用值，比策略S1的效用值要大.为了确定收益为50万元的效用值，可以适当提高S1成功的概率并继续询问：如果现在获利500万元的概率为0.8，损失300万的概率为0.2，那么你是否愿意冒一下风险，还是仍然宁可稳拿50万元呢？如果决策者这时愿意冒一下风险，则说明在决策者的心目中现在所提出的假想方案的效用值大于稳得50万元方案的效用值.这时再适当减小S1成功的概率再问：如果获利500万元的概率为0.75，获利（－300）万元的概率为0.25时，你是否愿意冒一下风险，还是宁可稳拿50万元？如果决策者这时认为这两者对他来说无所谓，都可以，这就说明在决策者的心目中“这两个方案的效用值相等”，那么我们就停止询问.由于已知u（－300）＝0，u（500）＝1，我们就可以确定50万元的效用值：

一般可以用插值方法来确定［a，b］中其他x的效用值u（x）：α，β∈［a，b］，若已知u（β）和u（α），α＜x＜β，如果通过对话不断修改pβ之值，直至最后发现决策者心目中“稳获利x的假想方案与获利β的概率为P＊、获利α的概率为（1－P＊）之假想方案的效用值是相等”的时候，则令

若已确定［a，b］中x1，x2，…，xn对应的效用值u（x1），u（x2），…，u（xn），那么就可以用一条光滑曲线把这些点（xi，u（xi））（i＝1，2，…，n）连接起来，这就是效用函数曲线（见图12－5）.

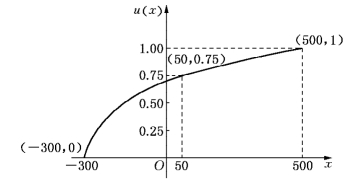
图12－5

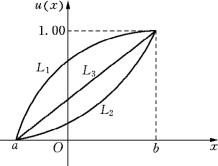
图12－6

不同的决策者对待风险的态度有所不同，因此会得到形状不同的效用曲线.一般有保守型（避险型）、冒险型（进取型）和中间型（无关型）3种类型.其对应的曲线如图12－6所示.

1.保守型

其对应的曲线如图12－6所示的曲线L1，这是一条向上凸起的曲线.它的特点是：当收益值较小时，效用值增加较快；而随着收益值的增大，效用值增加的速度越来越慢.它反映出相应的决策者讨厌风险、谨慎从事的特点，这是一个避免担风险的保守型决策者.

2.冒险型(www.daowen.com)

其对应的曲线如图12－6所示的曲线L2，这是一条向下凹进的曲线.它的特点是：当收益值较小时，效用值增加较为缓慢；而随着收益值的增大，效用值增加的速度越来越快.它反映出相应的决策者是一位喜欢冒险、锐意进取的决策者.

3.中间型

其对应的曲线如图12－6中的曲线L3，这是一条直线.它的特点是：收益值与效用值成正比例上升.它反映出相应的决策者是一位严格按照期望值准则的循规蹈矩的决策者.

但是，在实际决策过程中，决策者效用曲线可能是3种类型兼而有之，当收益变化时，决策者对待风险的态度也会发生变化.

例12－10　某农场考虑是否提早种植某种作物的决策问题.如果提早种，又不遇霜冻，则收入为45万元；如遇霜冻，则收入仅为10万元，遇霜冻的概率为0.4.如不提早种，又不遇霜冻，则收入为35万元；即使遇霜冻，受灾也轻，收入为25万元，遇霜冻的概率为0.2.问今年是否提早种植？

解　（1）绘制效用曲线.

现在a＝10，b＝45.于是，我们取u（45）＝1，u（10）＝0.我们采用对比提问法，得到效用曲线，如图12－7所示.

由图12－7可知u（35）＝0.5，u（25）＝0.25.

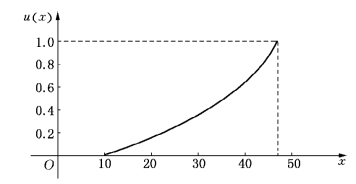
图12－7

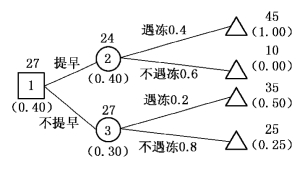
图12－8

（2）绘制决策树.如图12－8所示，△旁同时注上了收益和对应的效用值（带括号）.

在图12－8中，点②的期望效用值＝1×0.4＋0×0.6＝0.4；点③的期望效用值＝0.50×0.2＋0.25×0.8＝0.30，按期望效用值最大的准则，应选取“提早种”的策略，这是冒险型决策者所作的最优决策；而从决策树中我们不难看出根据收益期望值最大的原则是应该采用“不提早种”的策略.