有时我们关于自然状态的信息掌握得很少，无法估算出自然状态的概率分布，因而难以运用随机型决策方法.因此，这类非确定型决策，就要依据决策者的决策偏向进行决策，也就是说在这种情况下主要取决于决策者的主观意志和素质.

常用的处理这类非确定型决策问题的方法有：乐观值准则、悲观值准则、折中值准则、后悔值准则和等可能准则.我们结合实例来说明这5个准则.

例12－9　某电视机厂为下一年度作广告宣传需要进行投资.现考虑了4个方案：S1（维持今年水平）；S2（增加5万元）；S3（增加10万元）；S4（增加20万元）.未来电视机市场可能出现4种情况：N1（有较大上升）；N2（略有上升）；N3（与今年持平）；N4（有所下降）.收益f（Si，Nj）＝aij如表12－15所示，由于没有认可关于销售量的预测资料，试用各种不同的决策准则求出最优策略.

表12－15（单位：万元）

解　（1）乐观值决策准则.采用乐观值决策准则的决策者，属于敢担风险的进取型人才，对未来结果往往持乐观的态度，总是假设出现最有利的状态，认为即使出现不利的情况也未必会有多大的损失，但是一旦出现最有利的情况却能得到很大的收益.乐观值决策准则又称大中取大的准则.该准则为：

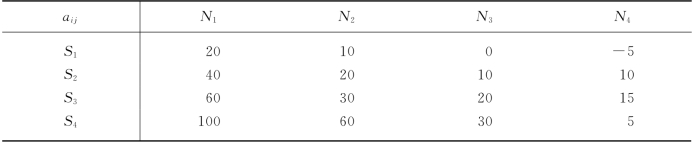
①根据效益矩阵A＝（aij），确定每一个策略可能获得的最好结果Mi：

②选取Sk，使得Mk＝max｛M1，M2，…，Mm｝.

我们用乐观值决策准则来求解例12－9.决策过程可以用表12－16来说明，其中用黑体字加括号标出的数是Mi中的最大值M4，因此应采用策略S4.

表12－16

（2）悲观值决策准则.采用悲观值决策准则的决策者，决策比较谨慎，不希望因为决策失误而造成失误，是从每一个可能出现的最差结果出发，通过分析多种最坏的可能结果，从中选择最好者，即从最不利的结果中选择最有利的结果.悲观值决策准则又称小中取大的准则.该准则为：

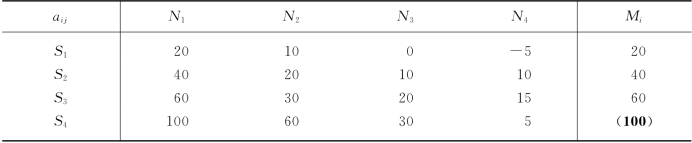
①根据效益矩阵A＝（aij），确定每一个策略可能得到的最坏结果mi：

②选取Sk，使得mk＝max｛m1，m2，…，mm｝.

我们用悲观值决策准则来求解例12.9.决策过程见表12－17，其中用黑体字加括号标出的数是诸mi中的最大值m3，因此采用策略S3.

表12－17

（3）折中值决策准则.折中值决策准则是介于悲观和乐观之间的决策准则，认为乐观值决策准则太冒险，悲观值决策准则太保守，那么考虑折中一下.即既不完全乐观，也不完全悲观，而是采用引进一个乐观系数λ（0≤λ≤1）来反映；而1－λ就称为悲观系数.该准则为：

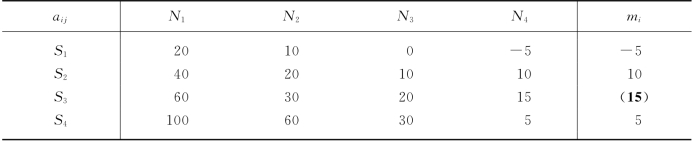
①根据乐观值准则中的Mi和悲观值中的mi计算折中值：

②选取Sk，使得

(www.daowen.com)

我们用λ＝0.3时的折中值决策准则来求解例12－9.决策过程见表12－18，可见应采用策略S4.

表12－18

（4）后悔值决策准则.在决策过程中，当某种状态可能出现时，决策者必然要选择使收益最大的策略，但决策者由于决策失误而没有选择收益最大的策略，就会感到后悔.后悔值决策准则的思想就是尽量减少决策后的后悔程度.衡量决策者后悔程度的一个指标，称为后悔值.事实上，相应于每对（Si，Ni）都可以定义一个后悔值rij：

其中ωj为决策者在状态Nj时可获得的最大收益，即

ωj＝max｛a1j，a2j，…，amj｝.该准则为：

①计算出后悔值rij（i＝1，2，…，m；j＝1，2，…，n）；

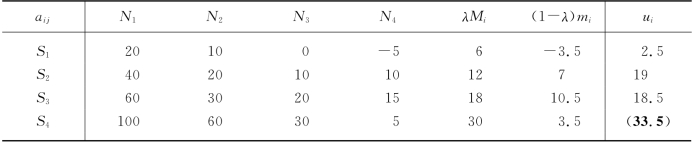
②对每个Si可能产生后悔最大的数值Ri：

③选取Sk，使得

我们用后悔值决策准则求解例12－9.决策过程见表12－19，采用策略S4.

表12－19

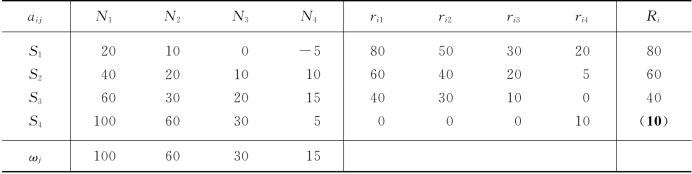
（5）等可能决策准则.在各种自然状态发生的概率总是相同的条件下，我们采用等可能决策准则来选择最优策略.该准则为：

①计算各策略在各自然状态等概率条件下的效益期望值：

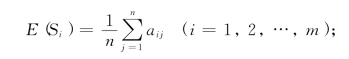
②由期望值中的最大者E（Sk），来确定相应的Sk作为最优策略.

我们用等可能决策准则求解例12－9.计算期望值：

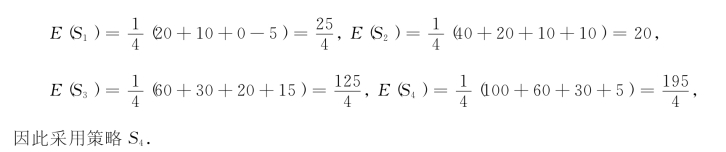
对非确定型决策问题，是因人、因时、因地选择的决策原则.在实际决策时，可根据具体情况同时选用几个不同的准则，然后将所得的结果进行分析比较，从而作出最后的选择.一般来说，总是在若干准则中，被选中多的策略应予以优先考虑.比如，例12－9求解中有4次决策为策略S4，所以S4应该是最优策略.