在随机型决策中，对自然状态Nj的概率分布P（Nj）所作估计的精确性，直接影响到决策的收益期望值.我们称概率分布P（Nj）（j＝1，2，…，n）为先验概率.为了提高先验概率的精确性，我们可以对决策系统进行一次试验或者调查，并根据试验或者调查的结果来修改先验概率，以便我们在计算新的各个相关收益期望值时可以把新的信息体现在模型中.我们称这些新的概率分布为后验概率.

在这里我们必须指出，在试验或者调查前出现的自然状态，和试验或者调查后出现的结果Z1，Z2，…，Zl未必相同.

例如，工厂生产的批量产品的自然状态有两种：N1表示为“好”的批量产品，N2表示为“不理想”的批量产品.现在知道先验概率P（N1）＝0.95，P（N2）＝0.05.但是这样的概率分布可信吗？为此工厂进行抽样检查，决定从某一批量产品中检验两件产品样本.于是结果有3种：

Z1为两件都是好的，Z2为有一件是好的，Z3为两件都是次品.

根据统计资料，“好”的批量产品中的次品率是4%，而“不理想”的批量产品中的次品率是10%.因为样本不是从“好”的批量产品中抽取，就是从“不理想”的批量产品中抽取，由于“好”的批量产品和“不理想”的批量产品中的次品率我们都已经估计，因此根据二项分布，条件概率P（Zk｜Nj）完全可以计算出来.然后，我们通过贝叶斯公式来计算条件概率P（Nj｜Zk）.如果抽样后的结果是Zk，我们就用P（Nj｜Zk）代替先验概率P（Nj）.这就是后验概率的意义.

我们再来看另一个实例.某公司对一块已经确定有石油资源的土地是否进行开采需要作出决策（自己开采或者出租）.估计该地出油量状态有N1，N2，N33种，概率分布已经进行了估算.现在公司希望对概率分布作进一步的修正，为此可以考虑是否进行一次“地震试验”.如果进行试验，那么地质结构的状态有Z1（好），Z2（较好），Z3（一般），Z4（差）4种.而条件概率P（Nj｜Zk）由统计资料完全可以确定.由于试验需要一笔费用，这样的试验是否需要做呢？

有了这样的准备知识以后，我们现在来给出贝叶斯决策方法.

为了使我们在利用期望值准则做决策的时候能够更加正确，我们考虑是否应花一笔费用进行试验或者调查，以得到有关新信息.然后利用这些新信息修正原先对P（Nj）所作的估计，并利用经过修正的概率分布再作决策.

我们假定试验或者调查后出现的结果是Z1，Z2，…，Zl，并且条件概率P（Zk｜Nj）能够估算出来.贝叶斯决策的基本步骤是：

（1）验前分析.决策者根据自己的经验和判断估计P（Nj），然后凭借这种验前概率分布和收益函数f（Si，Nj），计算E（Si），利用期望值准则作出决策.假定相应得出的收益期望值为E＊＝max｛E（Si）｜i＝1，2，…，m｝.

（2）预验分析.在实际试验或者调查前，可先对是否值得花一笔费用进行试验或者调查以获得新信息进行研究分析，从而作出是否试验或者调查的抉择.

（3）验后分析.在实际问题中，如果确实进行了试验或者调查，我们根据所得结果对验前概率分布作修正，得出验后概率分布，由新的概率分布和效益函数，计算新的E（Si），利用期望值准则重新作决策.

（4）阶段分析.为了提高决策的正确性，我们将试验或者调查搜索信息的过程划分为若干阶段，在每一阶段都作预验分析和验后分析.

那么在预验分析中如何进行抉择呢？

如果试验或者调查结果为Zk，我们利用概率论中的贝叶斯公式，可以算出在结果为Zk的条件下，自然状态为Nj的条件概率P（Nj｜Zk）：

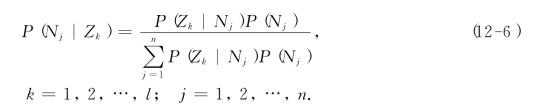
假设试验或者调查结果为Zk，由此用（12－6）算出概率P（Nj｜Zk）后，用它取代P（Nj），与收益函数f（Si，Nj）一起，利用期望值准则可以算出新的E（Si）：

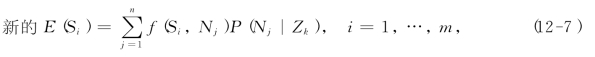
然后计算βk：

(www.daowen.com)

利用概率论中的全概率公式，可知试验或者调查结果为Zk的概率是：

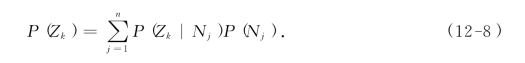
因此，估算出试验或者调查后决策所得的效益期望值为

而E＊＊－E＊就是如果进行试验或者调查使效益期望值增大的数值.显然，如果E＊＊－E＊大于试验或者调查的费用，那就可以认为试验或者调查是合算的.

如果在决策的过程中确实进行了试验或者调查，并出现结果Zk，那么P（Nj｜Zk）就是验后概率，βk－E＊就是这次试验或者调查真正增加出来的收益期望值.此时，如果考虑再作一轮新的试验或者调查，那么这次试验或者调查算得的验后概率可以作为下一次试验或者调查的验前概率来使用.

例12－8　在例12－1的基础上，我们考虑对市场进行调查，现假设调查结果为：

Z1（当前需求量较大），Z2（当前需求量中等），Z3（当前需求量较小）.

已知P（Zk｜Nj）如表12－12所示.问在什么条件下可以进行市场调查？请作贝叶斯决策.

表12－12

解　先根据式（12－8）求出P（Z1），P（Z2），P（Z3），如表12－13所示.再应用式（12－6）计算出P（Nj｜Zk），见表12－14.

表12－13

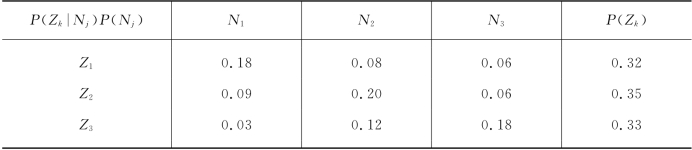
表12－14

最后，可得到如图12－4所示的决策树.由图12－4可知，E＊＊＝19.99万元，E＊＝17万元.因此，当调查费用不超过E＊＊－E＊＝19.99万元－17万元＝2.99万元的时候，可以进行调查.

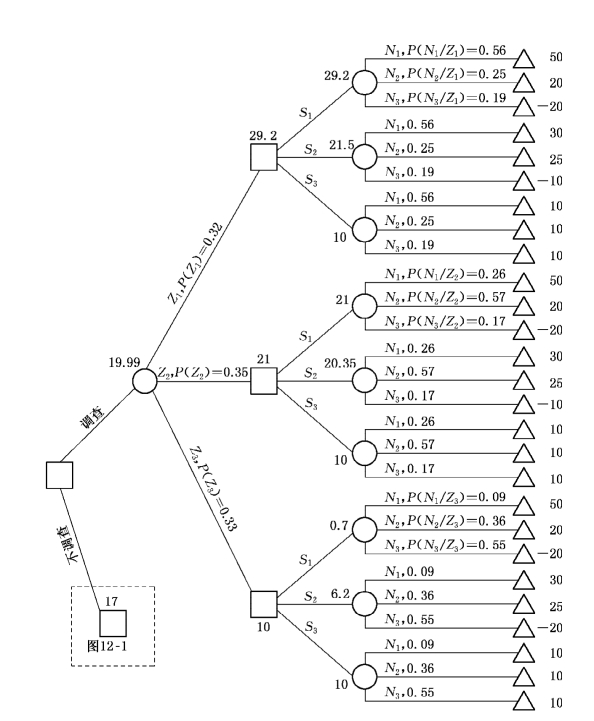
图12－4